Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/1453.html
1453. Maximum Number of Darts Inside of a Circular Dartboard
Level
Hard
Description
You have a very large square wall and a circular dartboard placed on the wall. You have been challenged to throw darts into the board blindfolded. Darts thrown at the wall are represented as an array of points on a 2D plane.
Return the maximum number of points that are within or lie on any circular dartboard of radius r.
Example 1:
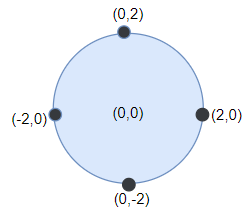
Input: points = [[-2,0],[2,0],[0,2],[0,-2]], r = 2
Output: 4
Explanation: Circle dartboard with center in (0,0) and radius = 2 contain all points.
Example 2:
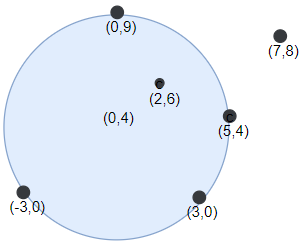
Input: points = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5
Output: 5
Explanation: Circle dartboard with center in (0,4) and radius = 5 contain all points except the point (7,8).
Example 3:
Input: points = [[-2,0],[2,0],[0,2],[0,-2]], r = 1
Output: 1
Example 4:
Input: points = [[1,2],[3,5],[1,-1],[2,3],[4,1],[1,3]], r = 2
Output: 4
Constraints:
1 <= points.length <= 100points[i].length == 2-10^4 <= points[i][0], points[i][1] <= 10^41 <= r <= 5000
Solution
For each point in points, use point as the center and r as the radius to draw a circle. Then for each pair of points in points, calculate the intersection points of the two circles. For each intersection point, draw a circle with radius r and count the number of points within or lie on the circle. During the process, store the maximum number of points within or lie on the circles. Finally, return the maximum number of points.
The precision needs to be considered. To determine whether the distance between two points is less than or equal to r, use r + 1e-5 instead since one of the points is represented in data type double.
-
class Solution { public int numPoints(int[][] points, int r) { int maxPoints = 1; int pointsCount = points.length; for (int i = 0; i < pointsCount; i++) { for (int j = i + 1; j < pointsCount; j++) { double[][] intersections = getIntersections(points[i], points[j], r); for (double[] intersection : intersections) { int pointsInCircle = 0; for (int[] point : points) { double distance = distance(intersection, point); if (distance <= r + 1e-5) pointsInCircle++; } maxPoints = Math.max(maxPoints, pointsInCircle); } } } return maxPoints; } public double[][] getIntersections(int[] point1, int[] point2, int radius) { int squaredDistance = squaredDistance(point1, point2); if (squaredDistance > radius * radius * 4) return new double[0][2]; else if (squaredDistance == radius * radius * 4) { double[] intersection = new double[2]; for (int i = 0; i < 2; i++) intersection[i] = (point1[i] + point2[i]) / 2.0; double[][] intersections = new double[1][2]; intersections[0] = intersection; return intersections; } else { double[] midPoint = new double[2]; for (int i = 0; i < 2; i++) midPoint[i] = (point1[i] + point2[i]) / 2.0; double remaining = Math.sqrt(radius * radius - squaredDistance / 4.0); int difference1 = point1[1] - point2[1]; int difference2 = point2[0] - point1[0]; double radian = Math.atan(1.0 * difference2 / difference1); double[] intersection0 = {midPoint[0] + remaining * Math.cos(radian), midPoint[1] + remaining * Math.sin(radian)}; double[] intersection1 = {midPoint[0] - remaining * Math.cos(radian), midPoint[1] - remaining * Math.sin(radian)}; double[][] intersections = new double[2][2]; intersections[0] = intersection0; intersections[1] = intersection1; return intersections; } } public int squaredDistance(int[] point1, int[] point2) { return (point2[0] - point1[0]) * (point2[0] - point1[0]) + (point2[1] - point1[1]) * (point2[1] - point1[1]); } public double distance(double[] point1, int[] point2) { return Math.sqrt((point2[0] - point1[0]) * (point2[0] - point1[0]) + (point2[1] - point1[1]) * (point2[1] - point1[1])); } } -
// OJ: https://leetcode.com/problems/maximum-number-of-darts-inside-of-a-circular-dartboard/ // Time: O(N^3) // Space: O(1) class Solution { inline double dist(const vector<double> &a, const vector<double> &b) { return sqrt(pow(a[0] - b[0], 2) + pow(a[1] - b[1], 2)); } vector<double> getPoint(const vector<double> &a, const vector<double> &b, double p, double q) { double x = (a[1] - b[1] + b[0] * q - a[0] * p) / (q - p); double y = a[1] + p * (x - a[0]); return {x, y}; } vector<vector<double>> getCenters(const vector<double> &a, const vector<double> &b, int r) { double d = dist(a, b); if (d > 2 * r) return {}; if (d == 2 * r) return { { (a[0] + b[0]) / 2, (a[1] + b[1]) / 2 } }; double theta = acos(d / 2 / r); double alpha = atan2(a[1] - b[1], a[0] - b[0]); double p = tan(alpha + theta), q = tan(alpha - theta); return { getPoint(a, b, p, q), getPoint(a, b, q, p) }; } public: int numPoints(vector<vector<int>>& A, int r) { int N = A.size(), ans = 0; for (int i = 0; i < N; ++i) { for (int j = 0; j < N; ++j) { for (auto ¢er : getCenters({(double)A[i][0], (double)A[i][1]}, {(double)A[j][0], (double)A[j][1]}, r)) { int cnt = 0; for (auto &p : A) { cnt += dist(center, {(double)p[0], (double)p[1]}) <= r + 0.00001; } ans = max(ans, cnt); } } } return ans; } }; -
class Solution: def numPoints(self, darts: list[list[int]], r: int) -> int: def countDarts(x, y): count = 0 for x1, y1 in darts: if dist((x, y), (x1, y1)) <= r + 1e-7: count += 1 return count def possibleCenters(x1, y1, x2, y2): dx, dy = x2 - x1, y2 - y1 d = sqrt(dx * dx + dy * dy) if d > 2 * r: return [] mid_x, mid_y = (x1 + x2) / 2, (y1 + y2) / 2 dist_to_center = sqrt(r * r - (d / 2) * (d / 2)) offset_x = dist_to_center * dy / d offset_y = dist_to_center * -dx / d return [ (mid_x + offset_x, mid_y + offset_y), (mid_x - offset_x, mid_y - offset_y), ] n = len(darts) max_darts = 1 for i in range(n): for j in range(i + 1, n): centers = possibleCenters( darts[i][0], darts[i][1], darts[j][0], darts[j][1] ) for center in centers: max_darts = max(max_darts, countDarts(center[0], center[1])) return max_darts