Welcome to Subscribe On Youtube
1382. Balance a Binary Search Tree
Description
Given the root of a binary search tree, return a balanced binary search tree with the same node values. If there is more than one answer, return any of them.
A binary search tree is balanced if the depth of the two subtrees of every node never differs by more than 1.
Example 1:
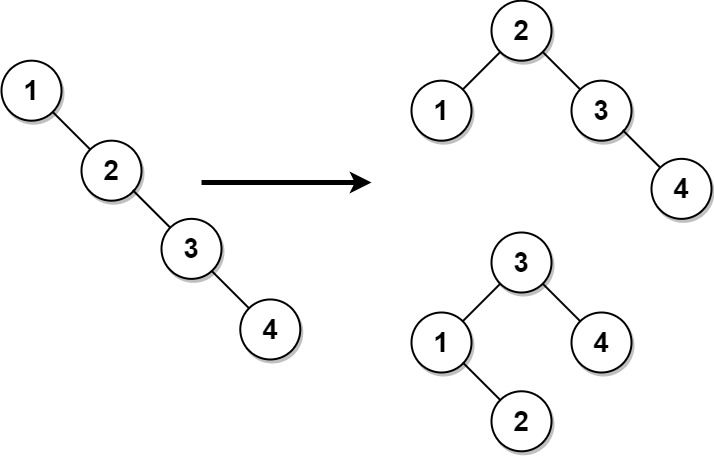
Input: root = [1,null,2,null,3,null,4,null,null] Output: [2,1,3,null,null,null,4] Explanation: This is not the only correct answer, [3,1,4,null,2] is also correct.
Example 2:
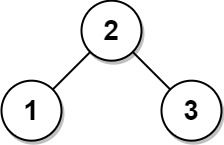
Input: root = [2,1,3] Output: [2,1,3]
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. 1 <= Node.val <= 105
Solutions
Solution 1: In-order Traversal + Construct Balanced Binary Search Tree
| Since the original tree is a binary search tree, we can save the result of the in-order traversal in an array $nums$. Then we design a function $build(i, j)$, which is used to construct a balanced binary search tree within the index range $[i, j]$ in $nums$. The answer is $build(0, | nums | - 1)$. |
The execution logic of the function $build(i, j)$ is as follows:
- If $i > j$, then the balanced binary search tree is empty, return an empty node;
- Otherwise, we take $mid = (i + j) / 2$ as the root node, then recursively build the left and right subtrees, and return the root node.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes in the binary search tree.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private List<Integer> nums = new ArrayList<>(); public TreeNode balanceBST(TreeNode root) { dfs(root); return build(0, nums.size() - 1); } private void dfs(TreeNode root) { if (root == null) { return; } dfs(root.left); nums.add(root.val); dfs(root.right); } private TreeNode build(int i, int j) { if (i > j) { return null; } int mid = (i + j) >> 1; TreeNode left = build(i, mid - 1); TreeNode right = build(mid + 1, j); return new TreeNode(nums.get(mid), left, right); } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: TreeNode* balanceBST(TreeNode* root) { dfs(root); return build(0, nums.size() - 1); } private: vector<int> nums; void dfs(TreeNode* root) { if (!root) { return; } dfs(root->left); nums.push_back(root->val); dfs(root->right); } TreeNode* build(int i, int j) { if (i > j) { return nullptr; } int mid = (i + j) >> 1; TreeNode* left = build(i, mid - 1); TreeNode* right = build(mid + 1, j); return new TreeNode(nums[mid], left, right); } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def balanceBST(self, root: TreeNode) -> TreeNode: def dfs(root: TreeNode): if root is None: return dfs(root.left) nums.append(root.val) dfs(root.right) def build(i: int, j: int) -> TreeNode: if i > j: return None mid = (i + j) >> 1 left = build(i, mid - 1) right = build(mid + 1, j) return TreeNode(nums[mid], left, right) nums = [] dfs(root) return build(0, len(nums) - 1) -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func balanceBST(root *TreeNode) *TreeNode { ans := []int{} var dfs func(*TreeNode) dfs = func(root *TreeNode) { if root == nil { return } dfs(root.Left) ans = append(ans, root.Val) dfs(root.Right) } var build func(i, j int) *TreeNode build = func(i, j int) *TreeNode { if i > j { return nil } mid := (i + j) >> 1 left := build(i, mid-1) right := build(mid+1, j) return &TreeNode{Val: ans[mid], Left: left, Right: right} } dfs(root) return build(0, len(ans)-1) } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function balanceBST(root: TreeNode | null): TreeNode | null { const nums: number[] = []; const dfs = (root: TreeNode | null): void => { if (root == null) { return; } dfs(root.left); nums.push(root.val); dfs(root.right); }; const build = (i: number, j: number): TreeNode | null => { if (i > j) { return null; } const mid: number = (i + j) >> 1; const left: TreeNode | null = build(i, mid - 1); const right: TreeNode | null = build(mid + 1, j); return new TreeNode(nums[mid], left, right); }; dfs(root); return build(0, nums.length - 1); }