Welcome to Subscribe On Youtube
1377. Frog Position After T Seconds
Description
Given an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices, it jumps randomly to one of them with the same probability. Otherwise, when the frog can not jump to any unvisited vertex, it jumps forever on the same vertex.
The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi.
Return the probability that after t seconds the frog is on the vertex target. Answers within 10-5 of the actual answer will be accepted.
Example 1:
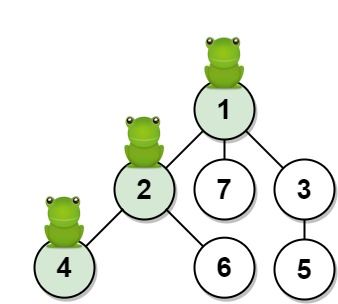
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4 Output: 0.16666666666666666 Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after second 1 and then jumping with 1/2 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666.
Example 2:
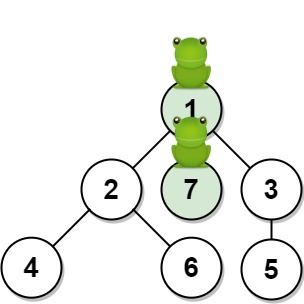
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7 Output: 0.3333333333333333 Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after second 1.
Constraints:
1 <= n <= 100edges.length == n - 1edges[i].length == 21 <= ai, bi <= n1 <= t <= 501 <= target <= n
Solutions
Solution 1: BFS
First, based on the undirected tree edges given in the problem, we construct an adjacency list $g$, where $g[u]$ represents all adjacent vertices of vertex $u$.
Then, we define the following data structures:
- Queue $q$, used to store the vertices and their probabilities for each round of search. Initially, $q = [(1, 1.0)]$, indicating that the probability of the frog being at vertex $1$ is $1.0$;
- Array $vis$, used to record whether each vertex has been visited. Initially, $vis[1] = true$, and all other elements are $false$.
Next, we start the breadth-first search.
In each round of search, we take out the head element $(u, p)$ of the queue, where $u$ and $p$ represent the current vertex and its probability, respectively. The number of unvisited adjacent vertices of the current vertex $u$ is denoted as $cnt$.
- If $u = target$, it means that the frog has reached the target vertex. At this time, we judge whether the frog reaches the target vertex in $t$ seconds, or it reaches the target vertex in less than $t$ seconds but cannot jump to other vertices (i.e., $t=0$ or $cnt=0$). If so, return $p$, otherwise return $0$.
- If $u \neq target$, we evenly distribute the probability $p$ to all unvisited adjacent vertices of $u$, then add these vertices to the queue $q$, and mark these vertices as visited.
At the end of a round of search, we decrease $t$ by $1$, and then continue the next round of search until the queue is empty or $t \lt 0$.
-
class Solution { public double frogPosition(int n, int[][] edges, int t, int target) { List<Integer>[] g = new List[n + 1]; Arrays.setAll(g, k -> new ArrayList<>()); for (var e : edges) { int u = e[0], v = e[1]; g[u].add(v); g[v].add(u); } Deque<Pair<Integer, Double>> q = new ArrayDeque<>(); q.offer(new Pair<>(1, 1.0)); boolean[] vis = new boolean[n + 1]; vis[1] = true; for (; !q.isEmpty() && t >= 0; --t) { for (int k = q.size(); k > 0; --k) { var x = q.poll(); int u = x.getKey(); double p = x.getValue(); int cnt = g[u].size() - (u == 1 ? 0 : 1); if (u == target) { return cnt * t == 0 ? p : 0; } for (int v : g[u]) { if (!vis[v]) { vis[v] = true; q.offer(new Pair<>(v, p / cnt)); } } } } return 0; } } -
class Solution { public: double frogPosition(int n, vector<vector<int>>& edges, int t, int target) { vector<vector<int>> g(n + 1); for (auto& e : edges) { int u = e[0], v = e[1]; g[u].push_back(v); g[v].push_back(u); } queue<pair<int, double>> q{ { {1, 1.0} }}; bool vis[n + 1]; memset(vis, false, sizeof(vis)); vis[1] = true; for (; q.size() && t >= 0; --t) { for (int k = q.size(); k; --k) { auto [u, p] = q.front(); q.pop(); int cnt = g[u].size() - (u != 1); if (u == target) { return cnt * t == 0 ? p : 0; } for (int v : g[u]) { if (!vis[v]) { vis[v] = true; q.push({v, p / cnt}); } } } } return 0; } }; -
class Solution: def frogPosition( self, n: int, edges: List[List[int]], t: int, target: int ) -> float: g = defaultdict(list) for u, v in edges: g[u].append(v) g[v].append(u) q = deque([(1, 1.0)]) vis = [False] * (n + 1) vis[1] = True while q and t >= 0: for _ in range(len(q)): u, p = q.popleft() cnt = len(g[u]) - int(u != 1) if u == target: return p if cnt * t == 0 else 0 for v in g[u]: if not vis[v]: vis[v] = True q.append((v, p / cnt)) t -= 1 return 0 -
func frogPosition(n int, edges [][]int, t int, target int) float64 { g := make([][]int, n+1) for _, e := range edges { u, v := e[0], e[1] g[u] = append(g[u], v) g[v] = append(g[v], u) } type pair struct { u int p float64 } q := []pair{ {1, 1} } vis := make([]bool, n+1) vis[1] = true for ; len(q) > 0 && t >= 0; t-- { for k := len(q); k > 0; k-- { u, p := q[0].u, q[0].p q = q[1:] cnt := len(g[u]) if u != 1 { cnt-- } if u == target { if cnt*t == 0 { return p } return 0 } for _, v := range g[u] { if !vis[v] { vis[v] = true q = append(q, pair{v, p / float64(cnt)}) } } } } return 0 } -
function frogPosition(n: number, edges: number[][], t: number, target: number): number { const g: number[][] = Array.from({ length: n + 1 }, () => []); for (const [u, v] of edges) { g[u].push(v); g[v].push(u); } const q: number[][] = [[1, 1]]; const vis: boolean[] = Array.from({ length: n + 1 }, () => false); vis[1] = true; for (; q.length > 0 && t >= 0; --t) { for (let k = q.length; k > 0; --k) { const [u, p] = q.shift()!; const cnt = g[u].length - (u === 1 ? 0 : 1); if (u === target) { return cnt * t === 0 ? p : 0; } for (const v of g[u]) { if (!vis[v]) { vis[v] = true; q.push([v, p / cnt]); } } } } return 0; } -
public class Solution { public double FrogPosition(int n, int[][] edges, int t, int target) { List<int>[] g = new List<int>[n + 1]; for (int i = 0; i < n + 1; i++) { g[i] = new List<int>(); } foreach (int[] e in edges) { int u = e[0], v = e[1]; g[u].Add(v); g[v].Add(u); } Queue<Tuple<int, double>> q = new Queue<Tuple<int, double>>(); q.Enqueue(new Tuple<int, double>(1, 1.0)); bool[] vis = new bool[n + 1]; vis[1] = true; for (; q.Count > 0 && t >= 0; --t) { for (int k = q.Count; k > 0; --k) { (var u, var p) = q.Dequeue(); int cnt = g[u].Count - (u == 1 ? 0 : 1); if (u == target) { return cnt * t == 0 ? p : 0; } foreach (int v in g[u]) { if (!vis[v]) { vis[v] = true; q.Enqueue(new Tuple<int, double>(v, p / cnt)); } } } } return 0; } }