1373. Maximum Sum BST in Binary Tree

Description

Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than the node's key.
Both the left and right subtrees must also be binary search trees.

Example 1:

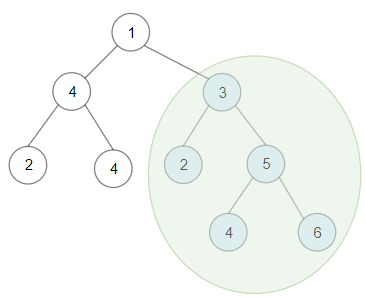
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2:

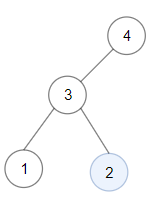
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Constraints:

The number of nodes in the tree is in the range [1, 4 * 10⁴].
-4 * 10⁴ <= Node.val <= 4 * 10⁴

Solutions

Solution 1: DFS

To determine whether a tree is a binary search tree, it needs to meet the following four conditions:

The left subtree is a binary search tree;
The right subtree is a binary search tree;
The maximum value of the left subtree is less than the value of the root node;
The minimum value of the right subtree is greater than the value of the root node.

Therefore, we design a function $dfs(root)$, the return value of the function is a quadruple $(bst, mi, mx, s)$, where:

The number $bst$ indicates whether the tree with $root$ as the root is a binary search tree. If it is a binary search tree, then $bst = 1$; otherwise $bst = 0$;
The number $mi$ represents the minimum value of the tree with $root$ as the root;
The number $mx$ represents the maximum value of the tree with $root$ as the root;
The number $s$ represents the sum of all nodes of the tree with $root$ as the root.

The execution logic of the function $dfs(root)$ is as follows:

If $root$ is an empty node, return $(1, +\infty, -\infty, 0)$, indicating that the empty tree is a binary search tree, the minimum value and maximum value are positive infinity and negative infinity respectively, and the sum of nodes is $0$.

Otherwise, recursively calculate the left subtree and right subtree of $root$, and get $(lbst, lmi, lmx, ls)$ and $(rbst, rmi, rmx, rs)$ respectively, then judge whether the $root$ node meets the conditions of the binary search tree.

If $lbst = 1$ and $rbst = 1$ and $lmx < root.val < rmi$, then the tree with $root$ as the root is a binary search tree, and the sum of nodes $s= ls + rs + root.val$. We update the answer $ans = \max(ans, s)$, and return $(1, \min(lmi, root.val), \max(rmx, root.val), s)$.

Otherwise, the tree with $root$ as the root is not a binary search tree, we return $(0, 0, 0, 0)$.

We call $dfs(root)$ in the main function. After execution, the answer is $ans$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes in the binary tree.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int ans;
    private final int inf = 1 << 30;

    public int maxSumBST(TreeNode root) {
        dfs(root);
        return ans;
    }

    private int[] dfs(TreeNode root) {
        if (root == null) {
            return new int[] {1, inf, -inf, 0};
        }
        var l = dfs(root.left);
        var r = dfs(root.right);
        int v = root.val;
        if (l[0] == 1 && r[0] == 1 && l[2] < v && r[1] > v) {
            int s = v + l[3] + r[3];
            ans = Math.max(ans, s);
            return new int[] {1, Math.min(l[1], v), Math.max(r[2], v), s};
        }
        return new int[4];
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxSumBST(TreeNode* root) {
        int ans = 0;
        const int inf = 1 << 30;

        function<vector<int>(TreeNode*)> dfs = [&](TreeNode* root) {
            if (!root) {
                return vector<int>{1, inf, -inf, 0};
            }
            auto l = dfs(root->left);
            auto r = dfs(root->right);
            int v = root->val;
            if (l[0] && r[0] && l[2] < v && v < r[1]) {
                int s = l[3] + r[3] + v;
                ans = max(ans, s);
                return vector<int>{1, min(l[1], v), max(r[2], v), s};
            }
            return vector<int>(4);
        };
        dfs(root);
        return ans;
    }
};

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxSumBST(self, root: Optional[TreeNode]) -> int:
        def dfs(root: Optional[TreeNode]) -> tuple:
            if root is None:
                return 1, inf, -inf, 0
            lbst, lmi, lmx, ls = dfs(root.left)
            rbst, rmi, rmx, rs = dfs(root.right)
            if lbst and rbst and lmx < root.val < rmi:
                nonlocal ans
                s = ls + rs + root.val
                ans = max(ans, s)
                return 1, min(lmi, root.val), max(rmx, root.val), s
            return 0, 0, 0, 0

        ans = 0
        dfs(root)
        return ans

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxSumBST(root *TreeNode) (ans int) {
	const inf = 1 << 30
	var dfs func(root *TreeNode) [4]int
	dfs = func(root *TreeNode) [4]int {
		if root == nil {
			return [4]int{1, inf, -inf, 0}
		}
		l, r := dfs(root.Left), dfs(root.Right)
		if l[0] == 1 && r[0] == 1 && l[2] < root.Val && root.Val < r[1] {
			s := l[3] + r[3] + root.Val
			ans = max(ans, s)
			return [4]int{1, min(l[1], root.Val), max(r[2], root.Val), s}
		}
		return [4]int{}
	}
	dfs(root)
	return
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function maxSumBST(root: TreeNode | null): number {
    const inf = 1 << 30;
    let ans = 0;
    const dfs = (root: TreeNode | null): [boolean, number, number, number] => {
        if (!root) {
            return [true, inf, -inf, 0];
        }
        const [lbst, lmi, lmx, ls] = dfs(root.left);
        const [rbst, rmi, rmx, rs] = dfs(root.right);
        if (lbst && rbst && lmx < root.val && root.val < rmi) {
            const s = ls + rs + root.val;
            ans = Math.max(ans, s);
            return [true, Math.min(lmi, root.val), Math.max(rmx, root.val), s];
        }
        return [false, 0, 0, 0];
    };
    dfs(root);
    return ans;
}

1373 - Maximum Sum BST in Binary Tree

1373. Maximum Sum BST in Binary Tree

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1373. Maximum Sum BST in Binary Tree

Description

Solutions

All Problems

All Solutions