Welcome to Subscribe On Youtube

1361. Validate Binary Tree Nodes

Description

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

 

Example 1:

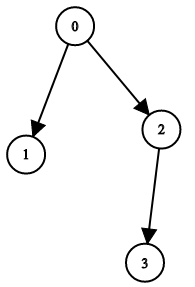
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

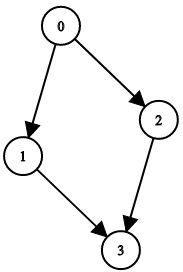
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

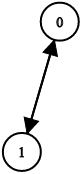
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

 

Constraints:

• n == leftChild.length == rightChild.length
• 1 <= n <= 104
• -1 <= leftChild[i], rightChild[i] <= n - 1

Solutions

Solution 1: Union-Find

We can traverse each node $i$ and its corresponding left and right children $l$, $r$, using an array $vis$ to record whether the node has a parent:

• If the child node already has a parent, it means there are multiple fathers, which does not meet the condition, so we return false directly.
• If the child node and the parent node are already in the same connected component, it means a cycle will be formed, which does not meet the condition, so we return false directly.
• Otherwise, we perform a union operation, set the corresponding position of the $vis$ array to true, and decrease the number of connected components by $1$.

After the traversal, we check whether the number of connected components in the union-find set is $1$. If it is, we return true, otherwise, we return false.

The time complexity is $O(n \times \alpha(n))$, and the space complexity is $O(n)$. Where $n$ is the number of nodes, and $\alpha(n)$ is the inverse Ackermann function, which is less than $5$.

• Java
• C++
• Python
• Go

• class Solution {
      private int[] p;
  
      public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {
          p = new int[n];
          for (int i = 0; i < n; ++i) {
              p[i] = i;
          }
          boolean[] vis = new boolean[n];
          for (int i = 0, m = n; i < m; ++i) {
              for (int j : new int[] {leftChild[i], rightChild[i]}) {
                  if (j != -1) {
                      if (vis[j] || find(i) == find(j)) {
                          return false;
                      }
                      p[find(i)] = find(j);
                      vis[j] = true;
                      --n;
                  }
              }
          }
          return n == 1;
      }
  
      private int find(int x) {
          if (p[x] != x) {
              p[x] = find(p[x]);
          }
          return p[x];
      }
  }
  

• class Solution {
  public:
      bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
          int p[n];
          iota(p, p + n, 0);
          bool vis[n];
          memset(vis, 0, sizeof(vis));
          function<int(int)> find = [&](int x) {
              return p[x] == x ? x : p[x] = find(p[x]);
          };
          for (int i = 0, m = n; i < m; ++i) {
              for (int j : {leftChild[i], rightChild[i]}) {
                  if (j != -1) {
                      if (vis[j] || find(i) == find(j)) {
                          return false;
                      }
                      p[find(i)] = find(j);
                      vis[j] = true;
                      --n;
                  }
              }
          }
          return n == 1;
      }
  };
  

• class Solution:
      def validateBinaryTreeNodes(
          self, n: int, leftChild: List[int], rightChild: List[int]
      ) -> bool:
          def find(x: int) -> int:
              if p[x] != x:
                  p[x] = find(p[x])
              return p[x]
  
          p = list(range(n))
          vis = [False] * n
          for i, (a, b) in enumerate(zip(leftChild, rightChild)):
              for j in (a, b):
                  if j != -1:
                      if vis[j] or find(i) == find(j):
                          return False
                      p[find(i)] = find(j)
                      vis[j] = True
                      n -= 1
          return n == 1
  
  

• func validateBinaryTreeNodes(n int, leftChild []int, rightChild []int) bool {
  	p := make([]int, n)
  	for i := range p {
  		p[i] = i
  	}
  	var find func(int) int
  	find = func(x int) int {
  		if p[x] != x {
  			p[x] = find(p[x])
  		}
  		return p[x]
  	}
  	vis := make([]bool, n)
  	for i, a := range leftChild {
  		for _, j := range []int{a, rightChild[i]} {
  			if j != -1 {
  				if vis[j] || find(i) == find(j) {
  					return false
  				}
  				p[find(i)] = find(j)
  				vis[j] = true
  				n--
  			}
  		}
  	}
  	return n == 1
  }
  

All Problems

All Solutions