Welcome to Subscribe On Youtube

1329. Sort the Matrix Diagonally

Description

A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].

Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.

 

Example 1:

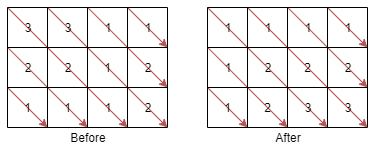
Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]

Example 2:

Input: mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
Output: [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• 1 <= mat[i][j] <= 100

Solutions

• Java
• C++
• Python
• Go
• TypeScript
• C#
• RenderScript

• class Solution {
      public int[][] diagonalSort(int[][] mat) {
          int m = mat.length, n = mat[0].length;
          for (int k = 0; k < Math.min(m, n) - 1; ++k) {
              for (int i = 0; i < m - 1; ++i) {
                  for (int j = 0; j < n - 1; ++j) {
                      if (mat[i][j] > mat[i + 1][j + 1]) {
                          int t = mat[i][j];
                          mat[i][j] = mat[i + 1][j + 1];
                          mat[i + 1][j + 1] = t;
                      }
                  }
              }
          }
          return mat;
      }
  }
  

• class Solution {
  public:
      vector<vector<int>> diagonalSort(vector<vector<int>>& mat) {
          int m = mat.size(), n = mat[0].size();
          for (int k = 0; k < min(m, n) - 1; ++k)
              for (int i = 0; i < m - 1; ++i)
                  for (int j = 0; j < n - 1; ++j)
                      if (mat[i][j] > mat[i + 1][j + 1])
                          swap(mat[i][j], mat[i + 1][j + 1]);
          return mat;
      }
  };
  

• class Solution:
      def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:
          m, n = len(mat), len(mat[0])
          for k in range(min(m, n) - 1):
              for i in range(m - 1):
                  for j in range(n - 1):
                      if mat[i][j] > mat[i + 1][j + 1]:
                          mat[i][j], mat[i + 1][j + 1] = mat[i + 1][j + 1], mat[i][j]
          return mat
  
  

• func diagonalSort(mat [][]int) [][]int {
  	m, n := len(mat), len(mat[0])
  	for k := 0; k < m-1 && k < n-1; k++ {
  		for i := 0; i < m-1; i++ {
  			for j := 0; j < n-1; j++ {
  				if mat[i][j] > mat[i+1][j+1] {
  					mat[i][j], mat[i+1][j+1] = mat[i+1][j+1], mat[i][j]
  				}
  			}
  		}
  	}
  	return mat
  }
  

• function diagonalSort(mat: number[][]): number[][] {
      const [m, n] = [mat.length, mat[0].length];
      const g: number[][] = Array.from({ length: m + n }, () => []);
      for (let i = 0; i < m; ++i) {
          for (let j = 0; j < n; ++j) {
              g[m - i + j].push(mat[i][j]);
          }
      }
      for (const e of g) {
          e.sort((a, b) => b - a);
      }
      for (let i = 0; i < m; ++i) {
          for (let j = 0; j < n; ++j) {
              mat[i][j] = g[m - i + j].pop()!;
          }
      }
      return mat;
  }
  
  

• public class Solution {
      public int[][] DiagonalSort(int[][] mat) {
          int m = mat.Length;
          int n = mat[0].Length;
          List<List<int>> g = new List<List<int>>();
          for (int i = 0; i < m + n; i++) {
              g.Add(new List<int>());
          }
          for (int i = 0; i < m; i++) {
              for (int j = 0; j < n; j++) {
                  g[m - i + j].Add(mat[i][j]);
              }
          }
          foreach (var e in g) {
              e.Sort((a, b) => b.CompareTo(a));
          }
          for (int i = 0; i < m; i++) {
              for (int j = 0; j < n; j++) {
                  int val = g[m - i + j][g[m - i + j].Count - 1];
                  g[m - i + j].RemoveAt(g[m - i + j].Count - 1);
                  mat[i][j] = val;
              }
          }
          return mat;
      }
  }
  

• impl Solution {
      pub fn diagonal_sort(mut mat: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
          let m = mat.len();
          let n = mat[0].len();
          let mut g: Vec<Vec<i32>> = vec![vec![]; m + n];
          for i in 0..m {
              for j in 0..n {
                  g[m - i + j].push(mat[i][j]);
              }
          }
          for e in &mut g {
              e.sort_by(|a, b| b.cmp(a));
          }
          for i in 0..m {
              for j in 0..n {
                  mat[i][j] = g[m - i + j].pop().unwrap();
              }
          }
          mat
      }
  }
  
  

All Problems

All Solutions