Welcome to Subscribe On Youtube
1260. Shift 2D Grid
Description
Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.
In one shift operation:
- Element at
grid[i][j]moves togrid[i][j + 1]. - Element at
grid[i][n - 1]moves togrid[i + 1][0]. - Element at
grid[m - 1][n - 1]moves togrid[0][0].
Return the 2D grid after applying shift operation k times.
Example 1:
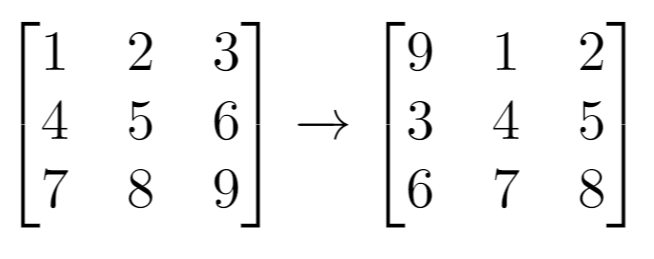
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]
Example 2:
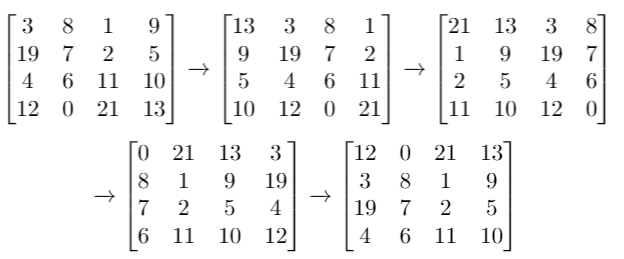
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]
Example 3:
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]
Constraints:
m == grid.lengthn == grid[i].length1 <= m <= 501 <= n <= 50-1000 <= grid[i][j] <= 10000 <= k <= 100
Solutions
Solution 1: Flattening the 2D Array
According to the problem description, if we flatten the 2D array into a 1D array, then each shift operation is to move the elements in the array one position to the right, with the last element moving to the first position of the array.
Therefore, we can flatten the 2D array into a 1D array, then calculate the final position $idx = (x, y)$ of each element, and update the answer array ans[x][y] = grid[i][j].
The time complexity is $O(m \times n)$, where $m$ and $n$ are the number of rows and columns in the grid array, respectively. We need to traverse the grid array once to calculate the final position of each element. Ignoring the space consumption of the answer array, the space complexity is $O(1)$.
-
class Solution { public List<List<Integer>> shiftGrid(int[][] grid, int k) { int m = grid.length, n = grid[0].length; List<List<Integer>> ans = new ArrayList<>(); for (int i = 0; i < m; ++i) { List<Integer> row = new ArrayList<>(); for (int j = 0; j < n; ++j) { row.add(0); } ans.add(row); } for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { int idx = (i * n + j + k) % (m * n); int x = idx / n, y = idx % n; ans.get(x).set(y, grid[i][j]); } } return ans; } } -
class Solution { public: vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) { int m = grid.size(), n = grid[0].size(); vector<vector<int>> ans(m, vector<int>(n)); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { int idx = (i * n + j + k) % (m * n); int x = idx / n, y = idx % n; ans[x][y] = grid[i][j]; } } return ans; } }; -
class Solution: def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]: m, n = len(grid), len(grid[0]) ans = [[0] * n for _ in range(m)] for i, row in enumerate(grid): for j, v in enumerate(row): x, y = divmod((i * n + j + k) % (m * n), n) ans[x][y] = v return ans -
func shiftGrid(grid [][]int, k int) [][]int { m, n := len(grid), len(grid[0]) ans := make([][]int, m) for i := range ans { ans[i] = make([]int, n) } for i := 0; i < m; i++ { for j := 0; j < n; j++ { idx := (i*n + j + k) % (m * n) x, y := idx/n, idx%n ans[x][y] = grid[i][j] } } return ans } -
function shiftGrid(grid: number[][], k: number): number[][] { const [m, n] = [grid.length, grid[0].length]; const ans: number[][] = Array.from({ length: m }, () => Array.from({ length: n }, () => 0)); for (let i = 0; i < m; ++i) { for (let j = 0; j < n; ++j) { const idx = (i * n + j + k) % (m * n); const [x, y] = [Math.floor(idx / n), idx % n]; ans[x][y] = grid[i][j]; } } return ans; }