Welcome to Subscribe On Youtube
1259. Handshakes That Don’t Cross
Description
You are given an even number of people numPeople that stand around a circle and each person shakes hands with someone else so that there are numPeople / 2 handshakes total.
Return the number of ways these handshakes could occur such that none of the handshakes cross.
Since the answer could be very large, return it modulo 109 + 7.
Example 1:

Input: numPeople = 4 Output: 2 Explanation: There are two ways to do it, the first way is [(1,2),(3,4)] and the second one is [(2,3),(4,1)].
Example 2:
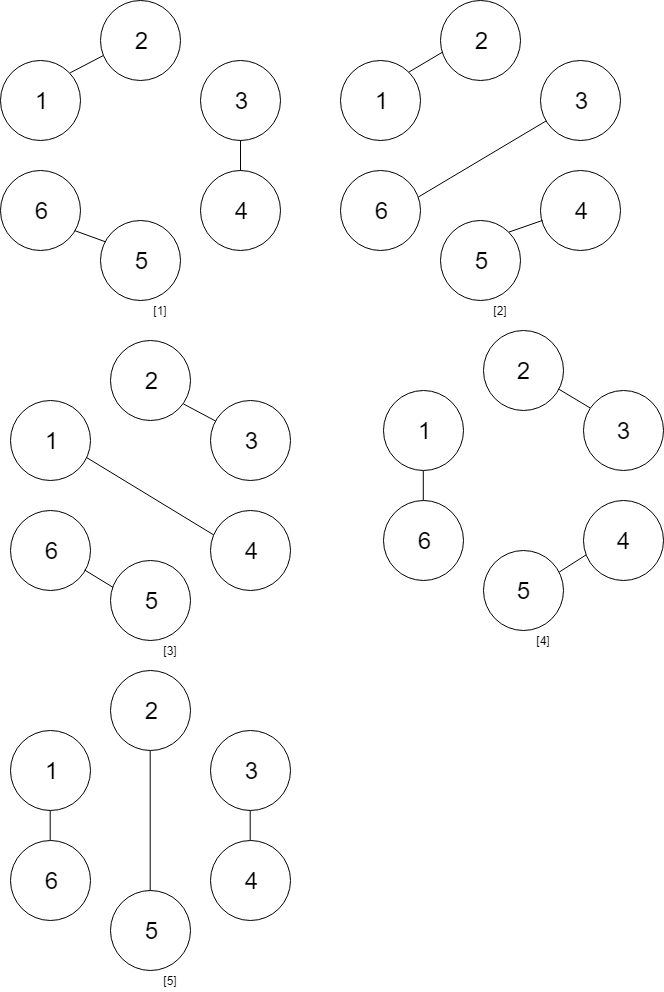
Input: numPeople = 6 Output: 5
Constraints:
2 <= numPeople <= 1000numPeopleis even.
Solutions
Solution 1: Memoization Search
We design a function $dfs(i)$, which represents the number of handshake schemes for $i$ people. The answer is $dfs(n)$.
The execution logic of the function $dfs(i)$ is as follows:
- If $i \lt 2$, then there is only one handshake scheme, which is not to shake hands, so return $1$.
- Otherwise, we can enumerate who the first person shakes hands with. Let the number of remaining people on the left be $l$, and the number of people on the right be $r=i-l-2$. Then we have $dfs(i)= \sum_{l=0}^{i-1} dfs(l) \times dfs(r)$.
To avoid repeated calculations, we use the method of memoization search.
The time complexity is $O(n^2)$, and the space complexity is $O(n)$. Where $n$ is the size of $numPeople$.
-
class Solution { private int[] f; private final int mod = (int) 1e9 + 7; public int numberOfWays(int numPeople) { f = new int[numPeople + 1]; return dfs(numPeople); } private int dfs(int i) { if (i < 2) { return 1; } if (f[i] != 0) { return f[i]; } for (int l = 0; l < i; l += 2) { int r = i - l - 2; f[i] = (int) ((f[i] + (1L * dfs(l) * dfs(r) % mod)) % mod); } return f[i]; } } -
class Solution { public: int numberOfWays(int numPeople) { const int mod = 1e9 + 7; int f[numPeople + 1]; memset(f, 0, sizeof(f)); function<int(int)> dfs = [&](int i) { if (i < 2) { return 1; } if (f[i]) { return f[i]; } for (int l = 0; l < i; l += 2) { int r = i - l - 2; f[i] = (f[i] + 1LL * dfs(l) * dfs(r) % mod) % mod; } return f[i]; }; return dfs(numPeople); } }; -
class Solution: def numberOfWays(self, numPeople: int) -> int: @cache def dfs(i: int) -> int: if i < 2: return 1 ans = 0 for l in range(0, i, 2): r = i - l - 2 ans += dfs(l) * dfs(r) ans %= mod return ans mod = 10**9 + 7 return dfs(numPeople) -
func numberOfWays(numPeople int) int { const mod int = 1e9 + 7 f := make([]int, numPeople+1) var dfs func(int) int dfs = func(i int) int { if i < 2 { return 1 } if f[i] != 0 { return f[i] } for l := 0; l < i; l += 2 { r := i - l - 2 f[i] = (f[i] + dfs(l)*dfs(r)) % mod } return f[i] } return dfs(numPeople) } -
function numberOfWays(numPeople: number): number { const mod = 10 ** 9 + 7; const f: number[] = Array(numPeople + 1).fill(0); const dfs = (i: number): number => { if (i < 2) { return 1; } if (f[i] !== 0) { return f[i]; } for (let l = 0; l < i; l += 2) { const r = i - l - 2; f[i] += Number((BigInt(dfs(l)) * BigInt(dfs(r))) % BigInt(mod)); f[i] %= mod; } return f[i]; }; return dfs(numPeople); }