Welcome to Subscribe On Youtube

1254. Number of Closed Islands

Description

Given a 2D grid consists of 0s (land) and 1s (water).  An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

 

Example 1:

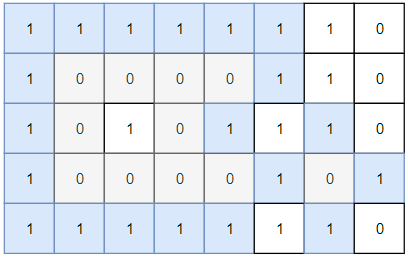
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation: 
Islands in gray are closed because they are completely surrounded by water (group of 1s).

Example 2:

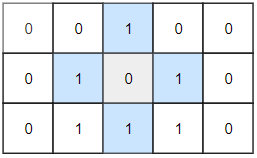
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

Example 3:

Input: grid = [[1,1,1,1,1,1,1],
               [1,0,0,0,0,0,1],
               [1,0,1,1,1,0,1],
               [1,0,1,0,1,0,1],
               [1,0,1,1,1,0,1],
               [1,0,0,0,0,0,1],
               [1,1,1,1,1,1,1]]
Output: 2

 

Constraints:

• 1 <= grid.length, grid[0].length <= 100
• 0 <= grid[i][j] <=1

Solutions

Solution 1: DFS

We traverse the matrix, and for each piece of land, we perform a depth-first search to find all the land connected to it. Then we check if there is any land on the boundary. If there is, it is not a closed island; otherwise, it is a closed island, and we increment the answer by one.

Finally, we return the answer.

The time complexity is $O(m\times n)$, and the space complexity is $O(m\times n)$. Where $m$ and $n$ are the number of rows and columns in the matrix, respectively.

Solution 2: Union-Find

We can use a union-find set to maintain each piece of connected land.

We traverse the matrix, if the current position is on the boundary, we connect it with the virtual node $m\times n$. If the current position is land, we connect it with the land below and to the right.

Then, we traverse the matrix again, for each piece of land, if its root node is itself, we increment the answer by one.

Finally, we return the answer.

The time complexity is $O(m\times n\times \alpha (m\times n))$, and the space complexity is $O(m\times n)$. Where $m$ and $n$ are the number of rows and columns in the matrix, respectively.

• Java
• C++
• Python
• Go
• TypeScript
• C#

• class Solution {
      private int m;
      private int n;
      private int[][] grid;
  
      public int closedIsland(int[][] grid) {
          m = grid.length;
          n = grid[0].length;
          this.grid = grid;
          int ans = 0;
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  if (grid[i][j] == 0) {
                      ans += dfs(i, j);
                  }
              }
          }
          return ans;
      }
  
      private int dfs(int i, int j) {
          int res = i > 0 && i < m - 1 && j > 0 && j < n - 1 ? 1 : 0;
          grid[i][j] = 1;
          int[] dirs = {-1, 0, 1, 0, -1};
          for (int k = 0; k < 4; ++k) {
              int x = i + dirs[k], y = j + dirs[k + 1];
              if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 0) {
                  res &= dfs(x, y);
              }
          }
          return res;
      }
  }
  

• class Solution {
  public:
      int closedIsland(vector<vector<int>>& grid) {
          int m = grid.size(), n = grid[0].size();
          int ans = 0;
          int dirs[5] = {-1, 0, 1, 0, -1};
          function<int(int, int)> dfs = [&](int i, int j) -> int {
              int res = i > 0 && i < m - 1 && j > 0 && j < n - 1 ? 1 : 0;
              grid[i][j] = 1;
              for (int k = 0; k < 4; ++k) {
                  int x = i + dirs[k], y = j + dirs[k + 1];
                  if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 0) {
                      res &= dfs(x, y);
                  }
              }
              return res;
          };
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  ans += grid[i][j] == 0 && dfs(i, j);
              }
          }
          return ans;
      }
  };
  

• class Solution:
      def closedIsland(self, grid: List[List[int]]) -> int:
          def dfs(i: int, j: int) -> int:
              res = int(0 < i < m - 1 and 0 < j < n - 1)
              grid[i][j] = 1
              for a, b in pairwise(dirs):
                  x, y = i + a, j + b
                  if 0 <= x < m and 0 <= y < n and grid[x][y] == 0:
                      res &= dfs(x, y)
              return res
  
          m, n = len(grid), len(grid[0])
          dirs = (-1, 0, 1, 0, -1)
          return sum(grid[i][j] == 0 and dfs(i, j) for i in range(m) for j in range(n))
  
  

• func closedIsland(grid [][]int) (ans int) {
  	m, n := len(grid), len(grid[0])
  	dirs := [5]int{-1, 0, 1, 0, -1}
  	var dfs func(i, j int) int
  	dfs = func(i, j int) int {
  		res := 1
  		if i == 0 || i == m-1 || j == 0 || j == n-1 {
  			res = 0
  		}
  		grid[i][j] = 1
  		for k := 0; k < 4; k++ {
  			x, y := i+dirs[k], j+dirs[k+1]
  			if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 0 {
  				res &= dfs(x, y)
  			}
  		}
  		return res
  	}
  	for i, row := range grid {
  		for j, v := range row {
  			if v == 0 {
  				ans += dfs(i, j)
  			}
  		}
  	}
  	return
  }
  

• function closedIsland(grid: number[][]): number {
      const m = grid.length;
      const n = grid[0].length;
      const dirs = [-1, 0, 1, 0, -1];
      const dfs = (i: number, j: number): number => {
          let res = i > 0 && j > 0 && i < m - 1 && j < n - 1 ? 1 : 0;
          grid[i][j] = 1;
          for (let k = 0; k < 4; ++k) {
              const [x, y] = [i + dirs[k], j + dirs[k + 1]];
              if (x >= 0 && y >= 0 && x < m && y < n && grid[x][y] === 0) {
                  res &= dfs(x, y);
              }
          }
          return res;
      };
      let ans = 0;
      for (let i = 0; i < m; ++i) {
          for (let j = 0; j < n; j++) {
              if (grid[i][j] === 0) {
                  ans += dfs(i, j);
              }
          }
      }
      return ans;
  }
  
  

• public class Solution {
      private int m;
      private int n;
      private int[][] grid;
  
      public int ClosedIsland(int[][] grid) {
          m = grid.Length;
          n = grid[0].Length;
          this.grid = grid;
          int ans = 0;
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  if (grid[i][j] == 0) {
                      ans += dfs(i, j);
                  }
              }
          }
          return ans;
      }
  
      private int dfs(int i, int j) {
          int res = i > 0 && i < m - 1 && j > 0 && j < n - 1 ? 1 : 0;
          grid[i][j] = 1;
          int[] dirs = {-1, 0, 1, 0, -1};
          for (int k = 0; k < 4; ++k) {
              int x = i + dirs[k], y = j + dirs[k + 1];
              if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 0) {
                  res &= dfs(x, y);
              }
          }
          return res;
      }
  }
  
  

All Problems

All Solutions