1240. Tiling a Rectangle with the Fewest Squares

Description

Given a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle.

Example 1:

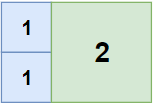
Input: n = 2, m = 3
Output: 3
Explanation: 3 squares are necessary to cover the rectangle.
2 (squares of 1x1)
1 (square of 2x2)

Example 2:

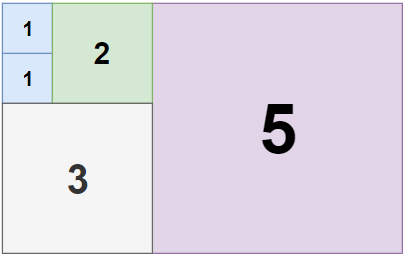
Input: n = 5, m = 8
Output: 5

Example 3:

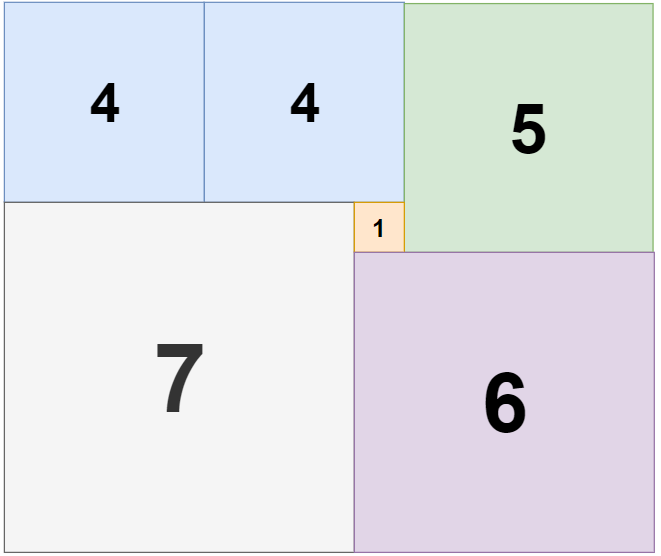
Input: n = 11, m = 13
Output: 6

Constraints:

1 <= n, m <= 13

Solutions

Solution 1: Recursive Backtracking + State Compression

We can perform recursive backtracking by position, during which we use a variable $t$ to record the current number of tiles used.

If $j = m$, i.e., the $i$-th row has been completely filled, then we recurse to the next row, i.e., $(i + 1, 0)$.
If $i = n$, it means that all positions have been filled, we update the answer and return.
If the current position $(i, j)$ has been filled, then directly recurse to the next position $(i, j + 1)$.
Otherwise, we enumerate the maximum square side length $w$ that the current position $(i, j)$ can fill, and fill all positions from $(i, j)$ to $(i + w - 1, j + w - 1)$, then recurse to the next position $(i, j + w)$. When backtracking, we need to clear all positions from $(i, j)$ to $(i + w - 1, j + w - 1)$.

Since each position only has two states: filled or not filled, we can use an integer to represent the current state. We use an integer array $filled$ of length $n$, where $filled[i]$ represents the state of the $i$-th row. If the $j$-th bit of $filled[i]$ is $1$, it means that the $i$-th row and the $j$-th column have been filled, otherwise it means not filled.

class Solution {
    private int n;
    private int m;
    private int[] filled;
    private int ans;

    public int tilingRectangle(int n, int m) {
        this.n = n;
        this.m = m;
        ans = n * m;
        filled = new int[n];
        dfs(0, 0, 0);
        return ans;
    }

    private void dfs(int i, int j, int t) {
        if (j == m) {
            ++i;
            j = 0;
        }
        if (i == n) {
            ans = t;
            return;
        }
        if ((filled[i] >> j & 1) == 1) {
            dfs(i, j + 1, t);
        } else if (t + 1 < ans) {
            int r = 0, c = 0;
            for (int k = i; k < n; ++k) {
                if ((filled[k] >> j & 1) == 1) {
                    break;
                }
                ++r;
            }
            for (int k = j; k < m; ++k) {
                if ((filled[i] >> k & 1) == 1) {
                    break;
                }
                ++c;
            }
            int mx = Math.min(r, c);
            for (int w = 1; w <= mx; ++w) {
                for (int k = 0; k < w; ++k) {
                    filled[i + w - 1] |= 1 << (j + k);
                    filled[i + k] |= 1 << (j + w - 1);
                }
                dfs(i, j + w, t + 1);
            }
            for (int x = i; x < i + mx; ++x) {
                for (int y = j; y < j + mx; ++y) {
                    filled[x] ^= 1 << y;
                }
            }
        }
    }
}

class Solution {
public:
    int tilingRectangle(int n, int m) {
        memset(filled, 0, sizeof(filled));
        this->n = n;
        this->m = m;
        ans = n * m;
        dfs(0, 0, 0);
        return ans;
    }

private:
    int filled[13];
    int n, m;
    int ans;

    void dfs(int i, int j, int t) {
        if (j == m) {
            ++i;
            j = 0;
        }
        if (i == n) {
            ans = t;
            return;
        }
        if (filled[i] >> j & 1) {
            dfs(i, j + 1, t);
        } else if (t + 1 < ans) {
            int r = 0, c = 0;
            for (int k = i; k < n; ++k) {
                if (filled[k] >> j & 1) {
                    break;
                }
                ++r;
            }
            for (int k = j; k < m; ++k) {
                if (filled[i] >> k & 1) {
                    break;
                }
                ++c;
            }
            int mx = min(r, c);
            for (int w = 1; w <= mx; ++w) {
                for (int k = 0; k < w; ++k) {
                    filled[i + w - 1] |= 1 << (j + k);
                    filled[i + k] |= 1 << (j + w - 1);
                }
                dfs(i, j + w, t + 1);
            }
            for (int x = i; x < i + mx; ++x) {
                for (int y = j; y < j + mx; ++y) {
                    filled[x] ^= 1 << y;
                }
            }
        }
    }
};

class Solution:
    def tilingRectangle(self, n: int, m: int) -> int:
        def dfs(i: int, j: int, t: int):
            nonlocal ans
            if j == m:
                i += 1
                j = 0
            if i == n:
                ans = t
                return
            if filled[i] >> j & 1:
                dfs(i, j + 1, t)
            elif t + 1 < ans:
                r = c = 0
                for k in range(i, n):
                    if filled[k] >> j & 1:
                        break
                    r += 1
                for k in range(j, m):
                    if filled[i] >> k & 1:
                        break
                    c += 1
                mx = r if r < c else c
                for w in range(1, mx + 1):
                    for k in range(w):
                        filled[i + w - 1] |= 1 << (j + k)
                        filled[i + k] |= 1 << (j + w - 1)
                    dfs(i, j + w, t + 1)
                for x in range(i, i + mx):
                    for y in range(j, j + mx):
                        filled[x] ^= 1 << y

        ans = n * m
        filled = [0] * n
        dfs(0, 0, 0)
        return ans

func tilingRectangle(n int, m int) int {
	ans := n * m
	filled := make([]int, n)
	var dfs func(i, j, t int)
	dfs = func(i, j, t int) {
		if j == m {
			i++
			j = 0
		}
		if i == n {
			ans = t
			return
		}
		if filled[i]>>j&1 == 1 {
			dfs(i, j+1, t)
		} else if t+1 < ans {
			var r, c int
			for k := i; k < n; k++ {
				if filled[k]>>j&1 == 1 {
					break
				}
				r++
			}
			for k := j; k < m; k++ {
				if filled[i]>>k&1 == 1 {
					break
				}
				c++
			}
			mx := min(r, c)
			for w := 1; w <= mx; w++ {
				for k := 0; k < w; k++ {
					filled[i+w-1] |= 1 << (j + k)
					filled[i+k] |= 1 << (j + w - 1)
				}
				dfs(i, j+w, t+1)
			}
			for x := i; x < i+mx; x++ {
				for y := j; y < j+mx; y++ {
					filled[x] ^= 1 << y
				}
			}
		}
	}
	dfs(0, 0, 0)
	return ans
}

function tilingRectangle(n: number, m: number): number {
    let ans = n * m;
    const filled: number[] = new Array(n).fill(0);
    const dfs = (i: number, j: number, t: number) => {
        if (j === m) {
            ++i;
            j = 0;
        }
        if (i === n) {
            ans = t;
            return;
        }
        if ((filled[i] >> j) & 1) {
            dfs(i, j + 1, t);
        } else if (t + 1 < ans) {
            let [r, c] = [0, 0];
            for (let k = i; k < n; ++k) {
                if ((filled[k] >> j) & 1) {
                    break;
                }
                ++r;
            }
            for (let k = j; k < m; ++k) {
                if ((filled[i] >> k) & 1) {
                    break;
                }
                ++c;
            }
            const mx = Math.min(r, c);
            for (let w = 1; w <= mx; ++w) {
                for (let k = 0; k < w; ++k) {
                    filled[i + w - 1] |= 1 << (j + k);
                    filled[i + k] |= 1 << (j + w - 1);
                }
                dfs(i, j + w, t + 1);
            }
            for (let x = i; x < i + mx; ++x) {
                for (let y = j; y < j + mx; ++y) {
                    filled[x] ^= 1 << y;
                }
            }
        }
    };
    dfs(0, 0, 0);
    return ans;
}

1240 - Tiling a Rectangle with the Fewest Squares

1240. Tiling a Rectangle with the Fewest Squares

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1240. Tiling a Rectangle with the Fewest Squares

Description

Solutions

All Problems

All Solutions