1214. Two Sum BSTs

Description

Given the roots of two binary search trees, root1 and root2, return true if and only if there is a node in the first tree and a node in the second tree whose values sum up to a given integer target.

Example 1:

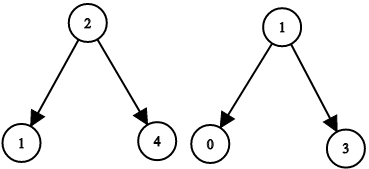
Input: root1 = [2,1,4], root2 = [1,0,3], target = 5
Output: true
Explanation: 2 and 3 sum up to 5.

Example 2:

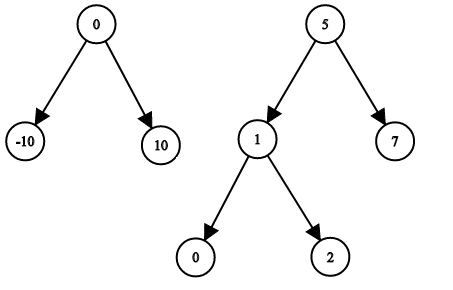
Input: root1 = [0,-10,10], root2 = [5,1,7,0,2], target = 18
Output: false

Constraints:

The number of nodes in each tree is in the range [1, 5000].
-10⁹ <= Node.val, target <= 10⁹

Solutions

Solution 1: In-order Traversal + Two Pointers

We perform in-order traversals on the two trees separately, obtaining two sorted arrays $nums[0]$ and $nums[1]$. Then we use a two-pointer method to determine whether there exist two numbers whose sum equals the target value. The two-pointer method is as follows:

Initialize two pointers $i$ and $j$, pointing to the left boundary of array $nums[0]$ and the right boundary of array $nums[1]$ respectively;

Each time, compare the sum $x = nums[0][i] + nums[1][j]$ with the target value. If $x = target$, return true; otherwise, if $x \lt target$, move $i$ one step to the right; otherwise, if $x \gt target$, move $j$ one step to the left.

The time complexity is $O(m + n)$, and the space complexity is $O(m + n)$. Here, $m$ and $n$ are the number of nodes in the two trees respectively.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private List<Integer>[] nums = new List[2];

    public boolean twoSumBSTs(TreeNode root1, TreeNode root2, int target) {
        Arrays.setAll(nums, k -> new ArrayList<>());
        dfs(root1, 0);
        dfs(root2, 1);
        int i = 0, j = nums[1].size() - 1;
        while (i < nums[0].size() && j >= 0) {
            int x = nums[0].get(i) + nums[1].get(j);
            if (x == target) {
                return true;
            }
            if (x < target) {
                ++i;
            } else {
                --j;
            }
        }
        return false;
    }

    private void dfs(TreeNode root, int i) {
        if (root == null) {
            return;
        }
        dfs(root.left, i);
        nums[i].add(root.val);
        dfs(root.right, i);
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool twoSumBSTs(TreeNode* root1, TreeNode* root2, int target) {
        vector<int> nums[2];
        function<void(TreeNode*, int)> dfs = [&](TreeNode* root, int i) {
            if (!root) {
                return;
            }
            dfs(root->left, i);
            nums[i].push_back(root->val);
            dfs(root->right, i);
        };
        dfs(root1, 0);
        dfs(root2, 1);
        int i = 0, j = nums[1].size() - 1;
        while (i < nums[0].size() && j >= 0) {
            int x = nums[0][i] + nums[1][j];
            if (x == target) {
                return true;
            }
            if (x < target) {
                ++i;
            } else {
                --j;
            }
        }
        return false;
    }
};

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def twoSumBSTs(
        self, root1: Optional[TreeNode], root2: Optional[TreeNode], target: int
    ) -> bool:
        def dfs(root: Optional[TreeNode], i: int):
            if root is None:
                return
            dfs(root.left, i)
            nums[i].append(root.val)
            dfs(root.right, i)

        nums = [[], []]
        dfs(root1, 0)
        dfs(root2, 1)
        i, j = 0, len(nums[1]) - 1
        while i < len(nums[0]) and ~j:
            x = nums[0][i] + nums[1][j]
            if x == target:
                return True
            if x < target:
                i += 1
            else:
                j -= 1
        return False

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func twoSumBSTs(root1 *TreeNode, root2 *TreeNode, target int) bool {
	nums := [2][]int{}
	var dfs func(*TreeNode, int)
	dfs = func(root *TreeNode, i int) {
		if root == nil {
			return
		}
		dfs(root.Left, i)
		nums[i] = append(nums[i], root.Val)
		dfs(root.Right, i)
	}
	dfs(root1, 0)
	dfs(root2, 1)
	i, j := 0, len(nums[1])-1
	for i < len(nums[0]) && j >= 0 {
		x := nums[0][i] + nums[1][j]
		if x == target {
			return true
		}
		if x < target {
			i++
		} else {
			j--
		}
	}
	return false
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function twoSumBSTs(root1: TreeNode | null, root2: TreeNode | null, target: number): boolean {
    const nums: number[][] = Array(2)
        .fill(0)
        .map(() => []);
    const dfs = (root: TreeNode | null, i: number) => {
        if (!root) {
            return;
        }
        dfs(root.left, i);
        nums[i].push(root.val);
        dfs(root.right, i);
    };
    dfs(root1, 0);
    dfs(root2, 1);
    let i = 0;
    let j = nums[1].length - 1;
    while (i < nums[0].length && j >= 0) {
        const x = nums[0][i] + nums[1][j];
        if (x === target) {
            return true;
        }
        if (x < target) {
            ++i;
        } else {
            --j;
        }
    }
    return false;
}

1214 - Two Sum BSTs

1214. Two Sum BSTs

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1214. Two Sum BSTs

Description

Solutions

All Problems

All Solutions