1192. Critical Connections in a Network

Description

There are n servers numbered from 0 to n - 1 connected by undirected server-to-server connections forming a network where connections[i] = [a_i, b_i] represents a connection between servers a_i and b_i. Any server can reach other servers directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some servers unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

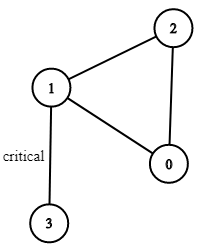
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

Example 2:

Input: n = 2, connections = [[0,1]]
Output: [[0,1]]

Constraints:

2 <= n <= 10⁵
n - 1 <= connections.length <= 10⁵
0 <= a_i, b_i <= n - 1
a_i != b_i
There are no repeated connections.

Solutions

Solution 1: Tarjan Algorithm

The “critical connections” in this problem can be considered as “bridges”.

“Bridges”: In a connected undirected graph, if removing a certain edge makes the graph disconnected, then this edge can be considered as a “bridge”.

Correspondingly, there is also the concept of “articulation points”.

“Articulation Points”: In a connected undirected graph, if removing a certain point and all edges connected to it makes the graph disconnected, then this point can be considered as an “articulation point”.

There is an algorithm called the Tarjan algorithm for finding “bridges” and “articulation points” in a graph. This algorithm uses a depth-first search (DFS) method that first recursively visits adjacent nodes and then visits the node itself. By recording the “order of visit: DFN” and updating the “earliest backtrackable node: low” when visiting the node itself after recursion ends, it can find the “bridges” and “articulation points” of the graph in $O(n)$ time. Also, this algorithm can be used to find strongly connected components in directed graphs.

class Solution {
    private int now;
    private List<Integer>[] g;
    private List<List<Integer>> ans = new ArrayList<>();
    private int[] dfn;
    private int[] low;

    public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        dfn = new int[n];
        low = new int[n];
        for (var e : connections) {
            int a = e.get(0), b = e.get(1);
            g[a].add(b);
            g[b].add(a);
        }
        tarjan(0, -1);
        return ans;
    }

    private void tarjan(int a, int fa) {
        dfn[a] = low[a] = ++now;
        for (int b : g[a]) {
            if (b == fa) {
                continue;
            }
            if (dfn[b] == 0) {
                tarjan(b, a);
                low[a] = Math.min(low[a], low[b]);
                if (low[b] > dfn[a]) {
                    ans.add(List.of(a, b));
                }
            } else {
                low[a] = Math.min(low[a], dfn[b]);
            }
        }
    }
}

class Solution {
public:
    vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) {
        int now = 0;
        vector<int> dfn(n);
        vector<int> low(n);
        vector<int> g[n];
        for (auto& e : connections) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        vector<vector<int>> ans;
        function<void(int, int)> tarjan = [&](int a, int fa) -> void {
            dfn[a] = low[a] = ++now;
            for (int b : g[a]) {
                if (b == fa) {
                    continue;
                }
                if (!dfn[b]) {
                    tarjan(b, a);
                    low[a] = min(low[a], low[b]);
                    if (low[b] > dfn[a]) {
                        ans.push_back({a, b});
                    }
                } else {
                    low[a] = min(low[a], dfn[b]);
                }
            }
        };
        tarjan(0, -1);
        return ans;
    }
};

class Solution:
    def criticalConnections(
        self, n: int, connections: List[List[int]]
    ) -> List[List[int]]:
        def tarjan(a: int, fa: int):
            nonlocal now
            now += 1
            dfn[a] = low[a] = now
            for b in g[a]:
                if b == fa:
                    continue
                if not dfn[b]:
                    tarjan(b, a)
                    low[a] = min(low[a], low[b])
                    if low[b] > dfn[a]:
                        ans.append([a, b])
                else:
                    low[a] = min(low[a], dfn[b])

        g = [[] for _ in range(n)]
        for a, b in connections:
            g[a].append(b)
            g[b].append(a)

        dfn = [0] * n
        low = [0] * n
        now = 0
        ans = []
        tarjan(0, -1)
        return ans

func criticalConnections(n int, connections [][]int) (ans [][]int) {
	now := 0
	g := make([][]int, n)
	dfn := make([]int, n)
	low := make([]int, n)
	for _, e := range connections {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	var tarjan func(int, int)
	tarjan = func(a, fa int) {
		now++
		dfn[a], low[a] = now, now
		for _, b := range g[a] {
			if b == fa {
				continue
			}
			if dfn[b] == 0 {
				tarjan(b, a)
				low[a] = min(low[a], low[b])
				if low[b] > dfn[a] {
					ans = append(ans, []int{a, b})
				}
			} else {
				low[a] = min(low[a], dfn[b])
			}
		}
	}
	tarjan(0, -1)
	return
}

function criticalConnections(n: number, connections: number[][]): number[][] {
    let now: number = 0;
    const g: number[][] = Array(n)
        .fill(0)
        .map(() => []);
    const dfn: number[] = Array(n).fill(0);
    const low: number[] = Array(n).fill(0);
    for (const [a, b] of connections) {
        g[a].push(b);
        g[b].push(a);
    }
    const ans: number[][] = [];
    const tarjan = (a: number, fa: number) => {
        dfn[a] = low[a] = ++now;
        for (const b of g[a]) {
            if (b === fa) {
                continue;
            }
            if (!dfn[b]) {
                tarjan(b, a);
                low[a] = Math.min(low[a], low[b]);
                if (low[b] > dfn[a]) {
                    ans.push([a, b]);
                }
            } else {
                low[a] = Math.min(low[a], dfn[b]);
            }
        }
    };
    tarjan(0, -1);
    return ans;
}

1192 - Critical Connections in a Network

1192. Critical Connections in a Network

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1192. Critical Connections in a Network

Description

Solutions

All Problems

All Solutions