Welcome to Subscribe On Youtube
1123. Lowest Common Ancestor of Deepest Leaves
Description
Given the root of a binary tree, return the lowest common ancestor of its deepest leaves.
Recall that:
- The node of a binary tree is a leaf if and only if it has no children
- The depth of the root of the tree is
0. if the depth of a node isd, the depth of each of its children isd + 1. - The lowest common ancestor of a set
Sof nodes, is the nodeAwith the largest depth such that every node inSis in the subtree with rootA.
Example 1:
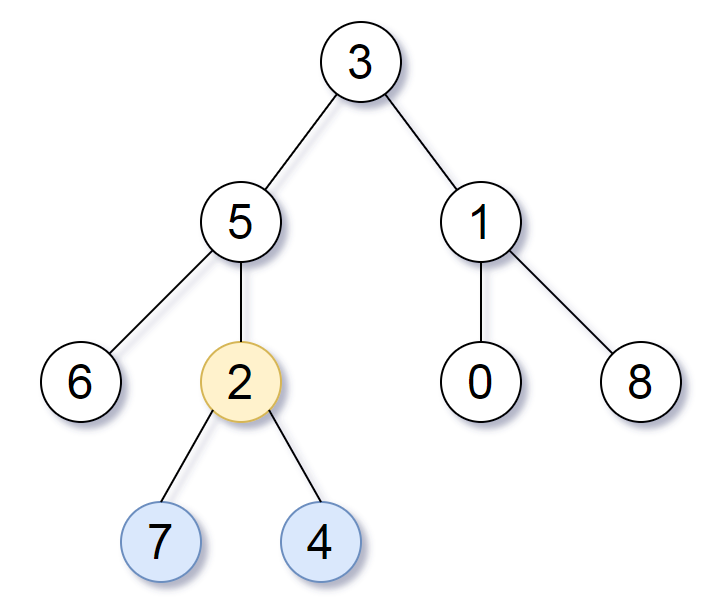
Input: root = [3,5,1,6,2,0,8,null,null,7,4] Output: [2,7,4] Explanation: We return the node with value 2, colored in yellow in the diagram. The nodes coloured in blue are the deepest leaf-nodes of the tree. Note that nodes 6, 0, and 8 are also leaf nodes, but the depth of them is 2, but the depth of nodes 7 and 4 is 3.
Example 2:
Input: root = [1] Output: [1] Explanation: The root is the deepest node in the tree, and it's the lca of itself.
Example 3:
Input: root = [0,1,3,null,2] Output: [2] Explanation: The deepest leaf node in the tree is 2, the lca of one node is itself.
Constraints:
- The number of nodes in the tree will be in the range
[1, 1000]. 0 <= Node.val <= 1000- The values of the nodes in the tree are unique.
Note: This question is the same as 865: https://leetcode.com/problems/smallest-subtree-with-all-the-deepest-nodes/
Solutions
Solution 1: DFS
We design a function dfs(root) that returns a tuple (l, d), where l is the deepest common ancestor of node root, and d is the depth of node root. The execution logic of the function dfs(root) is as follows:
- If
rootis null, return the tuple(None, 0); - Otherwise, we recursively call
dfs(root.left)anddfs(root.right), obtaining tuples(l, d1)and(r, d2). Ifd1 > d2, the deepest common ancestor ofrootisl, and the depth isd1 + 1; ifd1 < d2, the deepest common ancestor ofrootisr, and the depth isd2 + 1; ifd1 = d2, the deepest common ancestor ofrootisroot, and the depth isd1 + 1.
In the main function, we call dfs(root) and return the first element of its return value to get the deepest common ancestor node.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public TreeNode lcaDeepestLeaves(TreeNode root) { return dfs(root).getKey(); } private Pair<TreeNode, Integer> dfs(TreeNode root) { if (root == null) { return new Pair<>(null, 0); } Pair<TreeNode, Integer> l = dfs(root.left); Pair<TreeNode, Integer> r = dfs(root.right); int d1 = l.getValue(), d2 = r.getValue(); if (d1 > d2) { return new Pair<>(l.getKey(), d1 + 1); } if (d1 < d2) { return new Pair<>(r.getKey(), d2 + 1); } return new Pair<>(root, d1 + 1); } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: TreeNode* lcaDeepestLeaves(TreeNode* root) { return dfs(root).first; } pair<TreeNode*, int> dfs(TreeNode* root) { if (!root) { return {nullptr, 0}; } auto [l, d1] = dfs(root->left); auto [r, d2] = dfs(root->right); if (d1 > d2) { return {l, d1 + 1}; } if (d1 < d2) { return {r, d2 + 1}; } return {root, d1 + 1}; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def lcaDeepestLeaves(self, root: Optional[TreeNode]) -> Optional[TreeNode]: def dfs(root): if root is None: return None, 0 l, d1 = dfs(root.left) r, d2 = dfs(root.right) if d1 > d2: return l, d1 + 1 if d1 < d2: return r, d2 + 1 return root, d1 + 1 return dfs(root)[0] -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ type pair struct { first *TreeNode second int } func lcaDeepestLeaves(root *TreeNode) *TreeNode { var dfs func(root *TreeNode) pair dfs = func(root *TreeNode) pair { if root == nil { return pair{nil, 0} } l, r := dfs(root.Left), dfs(root.Right) d1, d2 := l.second, r.second if d1 > d2 { return pair{l.first, d1 + 1} } if d1 < d2 { return pair{r.first, d2 + 1} } return pair{root, d1 + 1} } return dfs(root).first } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function lcaDeepestLeaves(root: TreeNode | null): TreeNode | null { const dfs = (root: TreeNode | null): [TreeNode | null, number] => { if (root === null) { return [null, 0]; } const [l, d1] = dfs(root.left); const [r, d2] = dfs(root.right); if (d1 > d2) { return [l, d1 + 1]; } if (d1 < d2) { return [r, d2 + 1]; } return [root, d1 + 1]; }; return dfs(root)[0]; }