Welcome to Subscribe On Youtube
1102. Path With Maximum Minimum Value
Description
Given an m x n integer matrix grid, return the maximum score of a path starting at (0, 0) and ending at (m - 1, n - 1) moving in the 4 cardinal directions.
The score of a path is the minimum value in that path.
- For example, the score of the path
8 → 4 → 5 → 9is4.
Example 1:
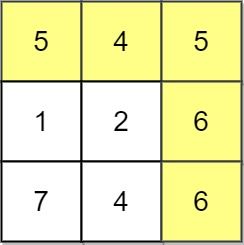
Input: grid = [[5,4,5],[1,2,6],[7,4,6]] Output: 4 Explanation: The path with the maximum score is highlighted in yellow.
Example 2:
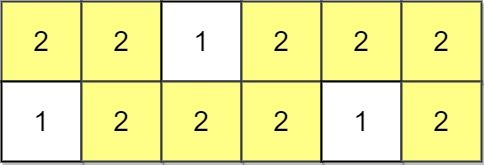
Input: grid = [[2,2,1,2,2,2],[1,2,2,2,1,2]] Output: 2
Example 3:
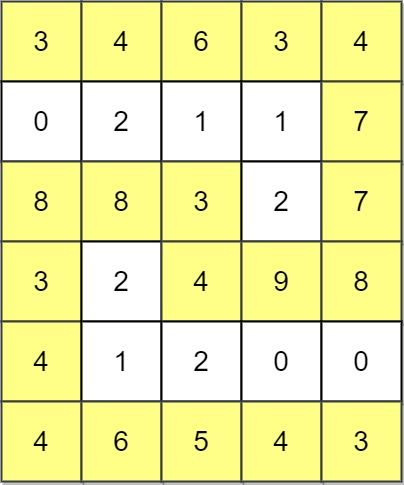
Input: grid = [[3,4,6,3,4],[0,2,1,1,7],[8,8,3,2,7],[3,2,4,9,8],[4,1,2,0,0],[4,6,5,4,3]] Output: 3
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 1000 <= grid[i][j] <= 109
Solutions
Solution 1: Sorting + Union-Find
First, we construct a triplet $(v, i, j)$ for each element in the matrix, where $v$ represents the element value, and $i$ and $j$ represent the row and column of the element in the matrix, respectively. Then we sort these triplets in descending order by element value and store them in a list $q$.
Next, we take out the triplets from $q$ in order, use the corresponding element value as the score of the path, and mark the position as visited. Then we check the four adjacent positions (up, down, left, and right) of this position. If an adjacent position has been visited, we merge this position with the current position. If we find that the position $(0, 0)$ and the position $(m - 1, n - 1)$ have been merged, we can directly return the score of the current path as the answer.
The time complexity is $O(m \times n \times (\log (m \times n) + \alpha(m \times n)))$, where $m$ and $n$ are the number of rows and columns of the matrix, respectively.
-
class Solution { private int[] p; public int maximumMinimumPath(int[][] grid) { int m = grid.length, n = grid[0].length; p = new int[m * n]; List<int[]> q = new ArrayList<>(); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { q.add(new int[] {grid[i][j], i, j}); p[i * n + j] = i * n + j; } } q.sort((a, b) -> b[0] - a[0]); boolean[][] vis = new boolean[m][n]; int[] dirs = {-1, 0, 1, 0, -1}; int ans = 0; for (int i = 0; find(0) != find(m * n - 1); ++i) { int[] t = q.get(i); vis[t[1]][t[2]] = true; ans = t[0]; for (int k = 0; k < 4; ++k) { int x = t[1] + dirs[k], y = t[2] + dirs[k + 1]; if (x >= 0 && x < m && y >= 0 && y < n && vis[x][y]) { p[find(x * n + y)] = find(t[1] * n + t[2]); } } } return ans; } private int find(int x) { if (p[x] != x) { p[x] = find(p[x]); } return p[x]; } } -
class Solution { public: int maximumMinimumPath(vector<vector<int>>& grid) { int m = grid.size(), n = grid[0].size(); vector<tuple<int, int, int>> q; vector<int> p(m * n); iota(p.begin(), p.end(), 0); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { q.emplace_back(grid[i][j], i, j); } } function<int(int)> find = [&](int x) { return p[x] == x ? x : p[x] = find(p[x]); }; sort(q.begin(), q.end(), greater<tuple<int, int, int>>()); int ans = 0; int dirs[5] = {-1, 0, 1, 0, -1}; bool vis[m][n]; memset(vis, false, sizeof(vis)); for (auto& [v, i, j] : q) { vis[i][j] = true; ans = v; for (int k = 0; k < 4; ++k) { int x = i + dirs[k], y = j + dirs[k + 1]; if (x >= 0 && x < m && y >= 0 && y < n && vis[x][y]) { p[find(x * n + y)] = find(i * n + j); } } if (find(0) == find(m * n - 1)) { break; } } return ans; } }; -
class Solution: def maximumMinimumPath(self, grid: List[List[int]]) -> int: def find(x: int) -> int: if p[x] != x: p[x] = find(p[x]) return p[x] m, n = len(grid), len(grid[0]) p = list(range(m * n)) q = [(v, i, j) for i, row in enumerate(grid) for j, v in enumerate(row)] q.sort() ans = 0 dirs = (-1, 0, 1, 0, -1) vis = set() while find(0) != find(m * n - 1): v, i, j = q.pop() ans = v vis.add((i, j)) for a, b in pairwise(dirs): x, y = i + a, j + b if (x, y) in vis: p[find(i * n + j)] = find(x * n + y) return ans -
func maximumMinimumPath(grid [][]int) (ans int) { m, n := len(grid), len(grid[0]) p := make([]int, m*n) vis := make([][]bool, m) q := [][3]int{} for i, row := range grid { vis[i] = make([]bool, n) for j, v := range row { p[i*n+j] = i*n + j q = append(q, [3]int{v, i, j}) } } sort.Slice(q, func(i, j int) bool { return q[i][0] > q[j][0] }) var find func(int) int find = func(x int) int { if p[x] != x { p[x] = find(p[x]) } return p[x] } dirs := [5]int{-1, 0, 1, 0, -1} for _, t := range q { v, i, j := t[0], t[1], t[2] ans = v vis[i][j] = true for k := 0; k < 4; k++ { x, y := i+dirs[k], j+dirs[k+1] if 0 <= x && x < m && 0 <= y && y < n && vis[x][y] { p[find(x*n+y)] = find(i*n + j) } } if find(0) == find(m*n-1) { break } } return } -
function maximumMinimumPath(grid: number[][]): number { const m = grid.length; const n = grid[0].length; const p: number[] = Array(m * n) .fill(0) .map((_, i) => i); const q: number[][] = []; for (let i = 0; i < m; ++i) { for (let j = 0; j < n; ++j) { q.push([grid[i][j], i, j]); } } q.sort((a, b) => b[0] - a[0]); const find = (x: number): number => { if (p[x] !== x) { p[x] = find(p[x]); } return p[x]; }; const dirs: number[] = [-1, 0, 1, 0, -1]; const vis: boolean[][] = Array(m) .fill(0) .map(() => Array(n).fill(false)); let ans = 0; for (let k = 0; find(0) !== find(m * n - 1); ++k) { const [t, i, j] = q[k]; ans = t; vis[i][j] = true; for (let d = 0; d < 4; ++d) { const [x, y] = [i + dirs[d], j + dirs[d + 1]]; if (x >= 0 && x < m && y >= 0 && y < n && vis[x][y]) { p[find(i * n + j)] = find(x * n + y); } } } return ans; } -
struct UnionFind { p: Vec<usize>, size: Vec<usize>, } impl UnionFind { fn new(n: usize) -> Self { let p: Vec<usize> = (0..n).collect(); let size = vec![1; n]; UnionFind { p, size } } fn find(&mut self, x: usize) -> usize { if self.p[x] != x { self.p[x] = self.find(self.p[x]); } self.p[x] } fn union(&mut self, a: usize, b: usize) { let pa = self.find(a); let pb = self.find(b); if pa != pb { if self.size[pa] > self.size[pb] { self.p[pb] = pa; self.size[pa] += self.size[pb]; } else { self.p[pa] = pb; self.size[pb] += self.size[pa]; } } } } impl Solution { pub fn maximum_minimum_path(grid: Vec<Vec<i32>>) -> i32 { let m = grid.len(); let n = grid[0].len(); let mut uf = UnionFind::new(m * n); let mut q: Vec<Vec<i32>> = Vec::new(); for i in 0..m { for j in 0..n { q.push(vec![grid[i][j], i as i32, j as i32]); } } q.sort_by(|a, b| b[0].cmp(&a[0])); let mut vis: Vec<Vec<bool>> = vec![vec![false; n]; m]; let dirs: [i32; 5] = [-1, 0, 1, 0, -1]; let mut ans = 0; for k in 0..q.len() { if uf.find(0) == uf.find(m * n - 1) { break; } let t = &q[k]; let (v, i, j) = (t[0], t[1] as usize, t[2] as usize); ans = v; vis[i][j] = true; for d in 0..4 { let x = (i as i32) + dirs[d]; let y = (j as i32) + dirs[d + 1]; if x >= 0 && x < (m as i32) && y >= 0 && y < (n as i32) && vis[x as usize][y as usize] { uf.union((x as usize) * n + (y as usize), i * n + j); } } } ans } }