Welcome to Subscribe On Youtube

1074. Number of Submatrices That Sum to Target

Description

Given a matrix and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.

 

Example 1:

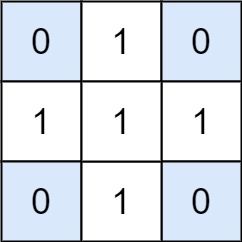
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.

Example 2:

Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.

Example 3:

Input: matrix = [[904]], target = 0
Output: 0

 

Constraints:

• 1 <= matrix.length <= 100
• 1 <= matrix[0].length <= 100
• -1000 <= matrix[i] <= 1000
• -10^8 <= target <= 10^8

Solutions

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      public int numSubmatrixSumTarget(int[][] matrix, int target) {
          int m = matrix.length, n = matrix[0].length;
          int ans = 0;
          for (int i = 0; i < m; ++i) {
              int[] col = new int[n];
              for (int j = i; j < m; ++j) {
                  for (int k = 0; k < n; ++k) {
                      col[k] += matrix[j][k];
                  }
                  ans += f(col, target);
              }
          }
          return ans;
      }
  
      private int f(int[] nums, int target) {
          Map<Integer, Integer> d = new HashMap<>();
          d.put(0, 1);
          int s = 0, cnt = 0;
          for (int x : nums) {
              s += x;
              cnt += d.getOrDefault(s - target, 0);
              d.merge(s, 1, Integer::sum);
          }
          return cnt;
      }
  }
  

• class Solution {
  public:
      int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
          int m = matrix.size(), n = matrix[0].size();
          int ans = 0;
          for (int i = 0; i < m; ++i) {
              vector<int> col(n);
              for (int j = i; j < m; ++j) {
                  for (int k = 0; k < n; ++k) {
                      col[k] += matrix[j][k];
                  }
                  ans += f(col, target);
              }
          }
          return ans;
      }
  
      int f(vector<int>& nums, int target) {
          unordered_map<int, int> d{ {0, 1} };
          int cnt = 0, s = 0;
          for (int& x : nums) {
              s += x;
              if (d.count(s - target)) {
                  cnt += d[s - target];
              }
              ++d[s];
          }
          return cnt;
      }
  };
  

• class Solution:
      def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
          def f(nums: List[int]) -> int:
              d = defaultdict(int)
              d[0] = 1
              cnt = s = 0
              for x in nums:
                  s += x
                  cnt += d[s - target]
                  d[s] += 1
              return cnt
  
          m, n = len(matrix), len(matrix[0])
          ans = 0
          for i in range(m):
              col = [0] * n
              for j in range(i, m):
                  for k in range(n):
                      col[k] += matrix[j][k]
                  ans += f(col)
          return ans
  
  

• func numSubmatrixSumTarget(matrix [][]int, target int) (ans int) {
  	m, n := len(matrix), len(matrix[0])
  	for i := 0; i < m; i++ {
  		col := make([]int, n)
  		for j := i; j < m; j++ {
  			for k := 0; k < n; k++ {
  				col[k] += matrix[j][k]
  			}
  			ans += f(col, target)
  		}
  	}
  	return
  }
  
  func f(nums []int, target int) (cnt int) {
  	d := map[int]int{0: 1}
  	s := 0
  	for _, x := range nums {
  		s += x
  		if v, ok := d[s-target]; ok {
  			cnt += v
  		}
  		d[s]++
  	}
  	return
  }
  

• function numSubmatrixSumTarget(matrix: number[][], target: number): number {
      const m = matrix.length;
      const n = matrix[0].length;
      let ans = 0;
      for (let i = 0; i < m; ++i) {
          const col: number[] = new Array(n).fill(0);
          for (let j = i; j < m; ++j) {
              for (let k = 0; k < n; ++k) {
                  col[k] += matrix[j][k];
              }
              ans += f(col, target);
          }
      }
      return ans;
  }
  
  function f(nums: number[], target: number): number {
      const d: Map<number, number> = new Map();
      d.set(0, 1);
      let cnt = 0;
      let s = 0;
      for (const x of nums) {
          s += x;
          if (d.has(s - target)) {
              cnt += d.get(s - target)!;
          }
          d.set(s, (d.get(s) || 0) + 1);
      }
      return cnt;
  }
  
  

All Problems

All Solutions