1020. Number of Enclaves

Description

You are given an m x n binary matrix grid, where 0 represents a sea cell and 1 represents a land cell.

A move consists of walking from one land cell to another adjacent (4-directionally) land cell or walking off the boundary of the grid.

Return the number of land cells in grid for which we cannot walk off the boundary of the grid in any number of moves.

Example 1:

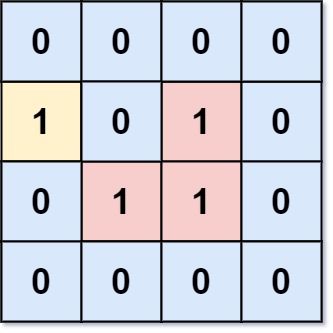
Input: grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
Output: 3
Explanation: There are three 1s that are enclosed by 0s, and one 1 that is not enclosed because its on the boundary.

Example 2:

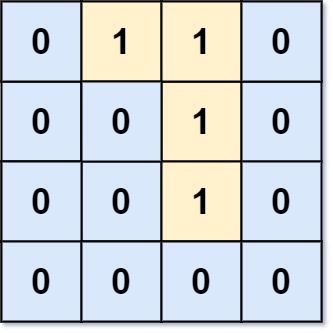
Input: grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
Output: 0
Explanation: All 1s are either on the boundary or can reach the boundary.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 500
grid[i][j] is either 0 or 1.

Solutions

class Solution {
    private int m;
    private int n;
    private int[][] grid;

    public int numEnclaves(int[][] grid) {
        this.grid = grid;
        m = grid.length;
        n = grid[0].length;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1 && (i == 0 || i == m - 1 || j == 0 || j == n - 1)) {
                    dfs(i, j);
                }
            }
        }
        int ans = 0;
        for (var row : grid) {
            for (var v : row) {
                ans += v;
            }
        }
        return ans;
    }

    private void dfs(int i, int j) {
        grid[i][j] = 0;
        int[] dirs = {-1, 0, 1, 0, -1};
        for (int k = 0; k < 4; ++k) {
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                dfs(x, y);
            }
        }
    }
}

class Solution {
public:
    int numEnclaves(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int dirs[5] = {-1, 0, 1, 0, -1};
        function<void(int, int)> dfs = [&](int i, int j) {
            grid[i][j] = 0;
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y]) {
                    dfs(x, y);
                }
            }
        };
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] && (i == 0 || i == m - 1 || j == 0 || j == n - 1)) {
                    dfs(i, j);
                }
            }
        }
        int ans = 0;
        for (auto& row : grid) {
            for (auto& v : row) {
                ans += v;
            }
        }
        return ans;
    }
};

class Solution:
    def numEnclaves(self, grid: List[List[int]]) -> int:
        def dfs(i, j):
            grid[i][j] = 0
            for a, b in pairwise(dirs):
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and grid[x][y]:
                    dfs(x, y)

        m, n = len(grid), len(grid[0])
        dirs = (-1, 0, 1, 0, -1)
        for i in range(m):
            for j in range(n):
                if grid[i][j] and (i == 0 or i == m - 1 or j == 0 or j == n - 1):
                    dfs(i, j)
        return sum(v for row in grid for v in row)

func numEnclaves(grid [][]int) (ans int) {
	m, n := len(grid), len(grid[0])
	dirs := [5]int{-1, 0, 1, 0, -1}
	var dfs func(i, j int)
	dfs = func(i, j int) {
		grid[i][j] = 0
		for k := 0; k < 4; k++ {
			x, y := i+dirs[k], j+dirs[k+1]
			if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 {
				dfs(x, y)
			}
		}
	}
	for i, row := range grid {
		for j, v := range row {
			if v == 1 && (i == 0 || i == m-1 || j == 0 || j == n-1) {
				dfs(i, j)
			}
		}
	}
	for _, row := range grid {
		for _, v := range row {
			ans += v
		}
	}
	return
}

function numEnclaves(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    const dirs = [-1, 0, 1, 0, -1];
    const dfs = (i: number, j: number) => {
        grid[i][j] = 0;
        for (let k = 0; k < 4; ++k) {
            const x = i + dirs[k];
            const y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y <= n && grid[x][y] === 1) {
                dfs(x, y);
            }
        }
    };
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (grid[i][j] === 1 && (i === 0 || i === m - 1 || j === 0 || j === n - 1)) {
                dfs(i, j);
            }
        }
    }
    let ans = 0;
    for (const row of grid) {
        for (const v of row) {
            ans += v;
        }
    }
    return ans;
}

impl Solution {
    fn dfs(grid: &mut Vec<Vec<i32>>, y: usize, x: usize) {
        if y >= grid.len() || x >= grid[0].len() || grid[y][x] == 0 {
            return;
        }
        grid[y][x] = 0;
        Solution::dfs(grid, y + 1, x);
        Solution::dfs(grid, y, x + 1);
        if y != 0 {
            Solution::dfs(grid, y - 1, x);
        }
        if x != 0 {
            Solution::dfs(grid, y, x - 1);
        }
    }
    pub fn num_enclaves(mut grid: Vec<Vec<i32>>) -> i32 {
        let mut res = 0;
        let m = grid.len();
        let n = grid[0].len();
        for i in 0..m {
            Solution::dfs(&mut grid, i, 0);
            Solution::dfs(&mut grid, i, n - 1);
        }
        for i in 0..n {
            Solution::dfs(&mut grid, 0, i);
            Solution::dfs(&mut grid, m - 1, i);
        }
        for i in 1..m - 1 {
            for j in 1..n - 1 {
                if grid[i][j] == 1 {
                    res += 1;
                }
            }
        }
        res
    }
}

1020 - Number of Enclaves

1020. Number of Enclaves

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1020. Number of Enclaves

Description

Solutions

All Problems

All Solutions