Welcome to Subscribe On Youtube
963. Minimum Area Rectangle II
Description
You are given an array of points in the X-Y plane points where points[i] = [xi, yi].
Return the minimum area of any rectangle formed from these points, with sides not necessarily parallel to the X and Y axes. If there is not any such rectangle, return 0.
Answers within 10-5 of the actual answer will be accepted.
Example 1:
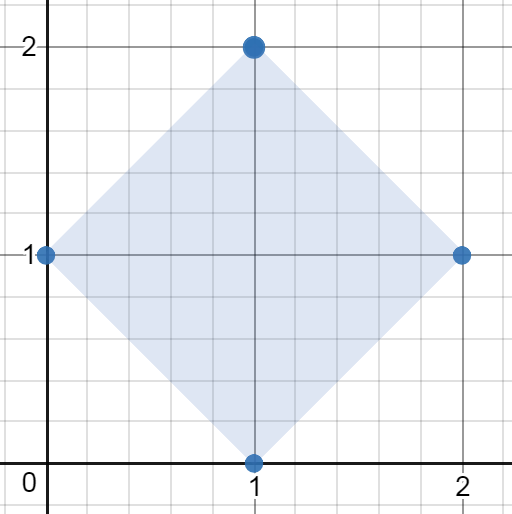
Input: points = [[1,2],[2,1],[1,0],[0,1]] Output: 2.00000 Explanation: The minimum area rectangle occurs at [1,2],[2,1],[1,0],[0,1], with an area of 2.
Example 2:
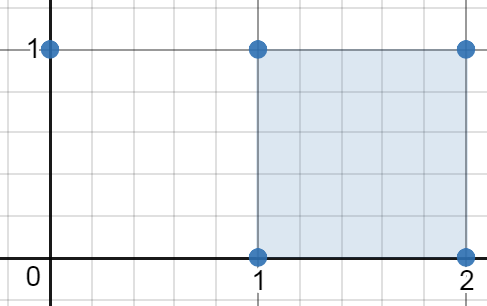
Input: points = [[0,1],[2,1],[1,1],[1,0],[2,0]] Output: 1.00000 Explanation: The minimum area rectangle occurs at [1,0],[1,1],[2,1],[2,0], with an area of 1.
Example 3:
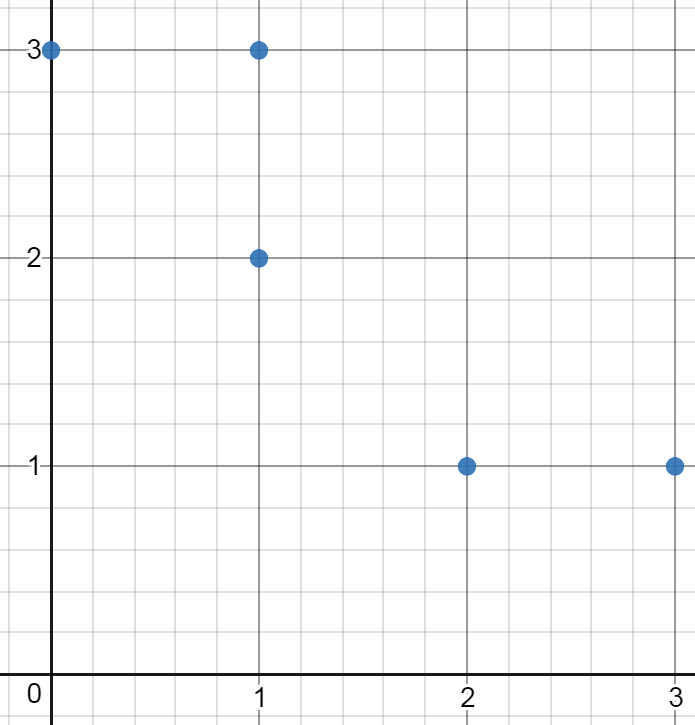
Input: points = [[0,3],[1,2],[3,1],[1,3],[2,1]] Output: 0 Explanation: There is no possible rectangle to form from these points.
Constraints:
1 <= points.length <= 50points[i].length == 20 <= xi, yi <= 4 * 104- All the given points are unique.
Solutions
-
class Solution { public double minAreaFreeRect(int[][] points) { int n = points.length; Set<Integer> s = new HashSet<>(n); for (int[] p : points) { s.add(f(p[0], p[1])); } double ans = Double.MAX_VALUE; for (int i = 0; i < n; ++i) { int x1 = points[i][0], y1 = points[i][1]; for (int j = 0; j < n; ++j) { if (j != i) { int x2 = points[j][0], y2 = points[j][1]; for (int k = j + 1; k < n; ++k) { if (k != i) { int x3 = points[k][0], y3 = points[k][1]; int x4 = x2 - x1 + x3, y4 = y2 - y1 + y3; if (s.contains(f(x4, y4))) { if ((x2 - x1) * (x3 - x1) + (y2 - y1) * (y3 - y1) == 0) { int ww = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1); int hh = (x3 - x1) * (x3 - x1) + (y3 - y1) * (y3 - y1); ans = Math.min(ans, Math.sqrt(1L * ww * hh)); } } } } } } } return ans == Double.MAX_VALUE ? 0 : ans; } private int f(int x, int y) { return x * 40001 + y; } } -
class Solution { public: double minAreaFreeRect(vector<vector<int>>& points) { auto f = [](int x, int y) { return x * 40001 + y; }; int n = points.size(); unordered_set<int> s; for (auto& p : points) { s.insert(f(p[0], p[1])); } double ans = 1e20; for (int i = 0; i < n; ++i) { int x1 = points[i][0], y1 = points[i][1]; for (int j = 0; j < n; ++j) { if (j != i) { int x2 = points[j][0], y2 = points[j][1]; for (int k = j + 1; k < n; ++k) { if (k != i) { int x3 = points[k][0], y3 = points[k][1]; int x4 = x2 - x1 + x3, y4 = y2 - y1 + y3; if (x4 >= 0 && x4 < 40000 && y4 >= 0 && y4 <= 40000 && s.count(f(x4, y4))) { if ((x2 - x1) * (x3 - x1) + (y2 - y1) * (y3 - y1) == 0) { int ww = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1); int hh = (x3 - x1) * (x3 - x1) + (y3 - y1) * (y3 - y1); ans = min(ans, sqrt(1LL * ww * hh)); } } } } } } } return ans == 1e20 ? 0 : ans; } }; -
class Solution: def minAreaFreeRect(self, points: List[List[int]]) -> float: s = {(x, y) for x, y in points} n = len(points) ans = inf for i in range(n): x1, y1 = points[i] for j in range(n): if j != i: x2, y2 = points[j] for k in range(j + 1, n): if k != i: x3, y3 = points[k] x4 = x2 - x1 + x3 y4 = y2 - y1 + y3 if (x4, y4) in s: v21 = (x2 - x1, y2 - y1) v31 = (x3 - x1, y3 - y1) if v21[0] * v31[0] + v21[1] * v31[1] == 0: w = sqrt(v21[0] ** 2 + v21[1] ** 2) h = sqrt(v31[0] ** 2 + v31[1] ** 2) ans = min(ans, w * h) return 0 if ans == inf else ans -
func minAreaFreeRect(points [][]int) float64 { n := len(points) f := func(x, y int) int { return x*40001 + y } s := map[int]bool{} for _, p := range points { s[f(p[0], p[1])] = true } ans := 1e20 for i := 0; i < n; i++ { x1, y1 := points[i][0], points[i][1] for j := 0; j < n; j++ { if j != i { x2, y2 := points[j][0], points[j][1] for k := j + 1; k < n; k++ { if k != i { x3, y3 := points[k][0], points[k][1] x4, y4 := x2-x1+x3, y2-y1+y3 if s[f(x4, y4)] { if (x2-x1)*(x3-x1)+(y2-y1)*(y3-y1) == 0 { ww := (x2-x1)*(x2-x1) + (y2-y1)*(y2-y1) hh := (x3-x1)*(x3-x1) + (y3-y1)*(y3-y1) ans = math.Min(ans, math.Sqrt(float64(ww*hh))) } } } } } } } if ans == 1e20 { return 0 } return ans } -
function minAreaFreeRect(points: number[][]): number { const n = points.length; const f = (x: number, y: number): number => x * 40001 + y; const s: Set<number> = new Set(); for (const [x, y] of points) { s.add(f(x, y)); } let ans = Number.MAX_VALUE; for (let i = 0; i < n; ++i) { const [x1, y1] = points[i]; for (let j = 0; j < n; ++j) { if (j !== i) { const [x2, y2] = points[j]; for (let k = j + 1; k < n; ++k) { if (k !== i) { const [x3, y3] = points[k]; const x4 = x2 - x1 + x3; const y4 = y2 - y1 + y3; if (s.has(f(x4, y4))) { if ((x2 - x1) * (x3 - x1) + (y2 - y1) * (y3 - y1) === 0) { const ww = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1); const hh = (x3 - x1) * (x3 - x1) + (y3 - y1) * (y3 - y1); ans = Math.min(ans, Math.sqrt(ww * hh)); } } } } } } } return ans === Number.MAX_VALUE ? 0 : ans; }