Welcome to Subscribe On Youtube

941. Valid Mountain Array

Description

Given an array of integers arr, return true if and only if it is a valid mountain array.

Recall that arr is a mountain array if and only if:

• arr.length >= 3
• There exists some i with 0 < i < arr.length - 1 such that:
  • arr[0] < arr[1] < ... < arr[i - 1] < arr[i]
  • arr[i] > arr[i + 1] > ... > arr[arr.length - 1]

 

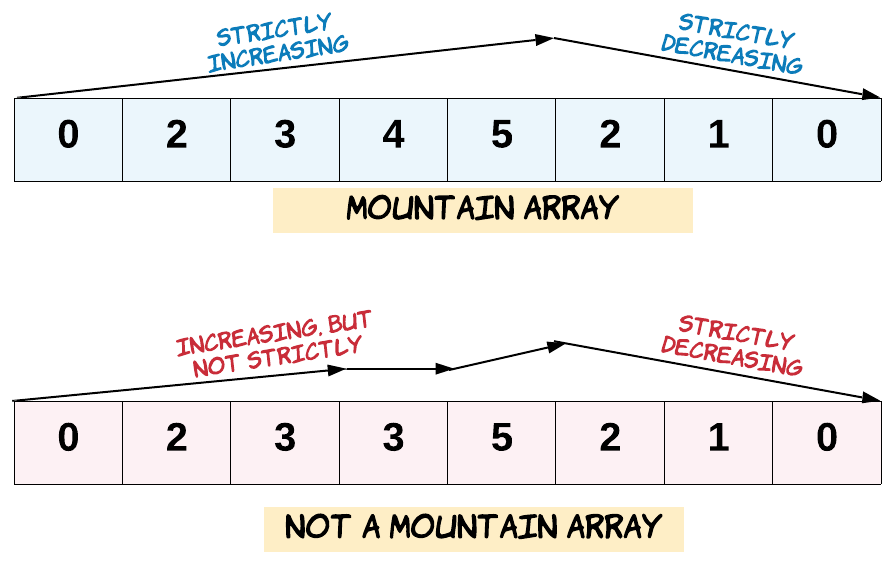
Example 1:

Input: arr = [2,1]
Output: false

Example 2:

Input: arr = [3,5,5]
Output: false

Example 3:

Input: arr = [0,3,2,1]
Output: true

 

Constraints:

• 1 <= arr.length <= 104
• 0 <= arr[i] <= 104

Solutions

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      public boolean validMountainArray(int[] arr) {
          int n = arr.length;
          if (n < 3) {
              return false;
          }
          int l = 0, r = n - 1;
          while (l + 1 < n - 1 && arr[l] < arr[l + 1]) {
              ++l;
          }
          while (r - 1 > 0 && arr[r] < arr[r - 1]) {
              --r;
          }
          return l == r;
      }
  }
  

• class Solution {
  public:
      bool validMountainArray(vector<int>& arr) {
          int n = arr.size();
          if (n < 3) return 0;
          int l = 0, r = n - 1;
          while (l + 1 < n - 1 && arr[l] < arr[l + 1]) ++l;
          while (r - 1 > 0 && arr[r] < arr[r - 1]) --r;
          return l == r;
      }
  };
  

• class Solution:
      def validMountainArray(self, arr: List[int]) -> bool:
          n = len(arr)
          if n < 3:
              return False
          l, r = 0, n - 1
          while l + 1 < n - 1 and arr[l] < arr[l + 1]:
              l += 1
          while r - 1 > 0 and arr[r] < arr[r - 1]:
              r -= 1
          return l == r
  
  

• func validMountainArray(arr []int) bool {
  	n := len(arr)
  	if n < 3 {
  		return false
  	}
  	l, r := 0, n-1
  	for l+1 < n-1 && arr[l] < arr[l+1] {
  		l++
  	}
  	for r-1 > 0 && arr[r] < arr[r-1] {
  		r--
  	}
  	return l == r
  }
  

• function validMountainArray(arr: number[]): boolean {
      const n = arr.length;
      if (n < 3) {
          return false;
      }
      let [i, j] = [0, n - 1];
      while (i + 1 < n - 1 && arr[i] < arr[i + 1]) {
          i++;
      }
      while (j - 1 > 0 && arr[j] < arr[j - 1]) {
          j--;
      }
      return i === j;
  }
  
  

All Problems

All Solutions