Welcome to Subscribe On Youtube
935. Knight Dialer
Description
The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:
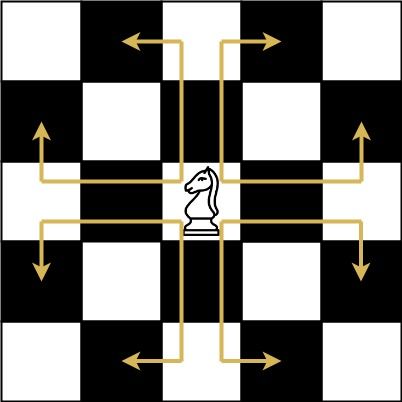
We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).
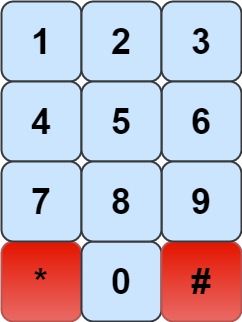
Given an integer n, return how many distinct phone numbers of length n we can dial.
You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.
As the answer may be very large, return the answer modulo 109 + 7.
Example 1:
Input: n = 1 Output: 10 Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
Example 2:
Input: n = 2 Output: 20 Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]
Example 3:
Input: n = 3131 Output: 136006598 Explanation: Please take care of the mod.
Constraints:
1 <= n <= 5000
Solutions
-
class Solution { private static final int MOD = (int) 1e9 + 7; public int knightDialer(int n) { if (n == 1) { return 10; } long[] f = new long[10]; Arrays.fill(f, 1); while (--n > 0) { long[] t = new long[10]; t[0] = f[4] + f[6]; t[1] = f[6] + f[8]; t[2] = f[7] + f[9]; t[3] = f[4] + f[8]; t[4] = f[0] + f[3] + f[9]; t[6] = f[0] + f[1] + f[7]; t[7] = f[2] + f[6]; t[8] = f[1] + f[3]; t[9] = f[2] + f[4]; for (int i = 0; i < 10; ++i) { f[i] = t[i] % MOD; } } long ans = 0; for (long v : f) { ans = (ans + v) % MOD; } return (int) ans; } } -
using ll = long long; class Solution { public: int knightDialer(int n) { if (n == 1) return 10; int mod = 1e9 + 7; vector<ll> f(10, 1ll); while (--n) { vector<ll> t(10); t[0] = f[4] + f[6]; t[1] = f[6] + f[8]; t[2] = f[7] + f[9]; t[3] = f[4] + f[8]; t[4] = f[0] + f[3] + f[9]; t[6] = f[0] + f[1] + f[7]; t[7] = f[2] + f[6]; t[8] = f[1] + f[3]; t[9] = f[2] + f[4]; for (int i = 0; i < 10; ++i) f[i] = t[i] % mod; } ll ans = accumulate(f.begin(), f.end(), 0ll); return (int) (ans % mod); } }; -
class Solution: def knightDialer(self, n: int) -> int: if n == 1: return 10 f = [1] * 10 for _ in range(n - 1): t = [0] * 10 t[0] = f[4] + f[6] t[1] = f[6] + f[8] t[2] = f[7] + f[9] t[3] = f[4] + f[8] t[4] = f[0] + f[3] + f[9] t[6] = f[0] + f[1] + f[7] t[7] = f[2] + f[6] t[8] = f[1] + f[3] t[9] = f[2] + f[4] f = t return sum(t) % (10**9 + 7) -
func knightDialer(n int) int { if n == 1 { return 10 } f := make([]int, 10) for i := range f { f[i] = 1 } mod := int(1e9) + 7 for i := 1; i < n; i++ { t := make([]int, 10) t[0] = f[4] + f[6] t[1] = f[6] + f[8] t[2] = f[7] + f[9] t[3] = f[4] + f[8] t[4] = f[0] + f[3] + f[9] t[6] = f[0] + f[1] + f[7] t[7] = f[2] + f[6] t[8] = f[1] + f[3] t[9] = f[2] + f[4] for j, v := range t { f[j] = v % mod } } ans := 0 for _, v := range f { ans = (ans + v) % mod } return ans } -
function knightDialer(n: number): number { const MOD: number = 1e9 + 7; if (n === 1) { return 10; } const f: number[] = new Array(10).fill(1); while (--n > 0) { const t: number[] = new Array(10).fill(0); t[0] = f[4] + f[6]; t[1] = f[6] + f[8]; t[2] = f[7] + f[9]; t[3] = f[4] + f[8]; t[4] = f[0] + f[3] + f[9]; t[6] = f[0] + f[1] + f[7]; t[7] = f[2] + f[6]; t[8] = f[1] + f[3]; t[9] = f[2] + f[4]; for (let i = 0; i < 10; ++i) { f[i] = t[i] % MOD; } } let ans: number = 0; for (const v of f) { ans = (ans + v) % MOD; } return ans; } -
public class Solution { public int KnightDialer(int n) { if (n == 1) return 10; int A = 4; int B = 2; int C = 2; int D = 1; int MOD = (int)1e9 + 7; for (int i = 0; i < n - 1; i++) { int tempA = A; int tempB = B; int tempC = C; int tempD = D; A = ((2 * tempB) % MOD + (2 * tempC) % MOD) % MOD; B = tempA; C = (tempA + (2 * tempD) % MOD) % MOD; D = tempC; } int ans = (A + B) % MOD; ans = (ans + C) % MOD; return (ans + D) % MOD; } } -
class Solution { private final int mod = (int) 1e9 + 7; private final int[][] base = {{0, 0, 0, 0, 1, 0, 1, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 1, 0, 1, 0}, {0, 0, 0, 0, 0, 0, 0, 1, 0, 1}, {0, 0, 0, 0, 1, 0, 0, 0, 1, 0}, {1, 0, 0, 1, 0, 0, 0, 0, 0, 1}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 1, 0, 0, 0, 0, 0, 1, 0, 0}, {0, 0, 1, 0, 0, 0, 1, 0, 0, 0}, {0, 1, 0, 1, 0, 0, 0, 0, 0, 0}, {0, 0, 1, 0, 1, 0, 0, 0, 0, 0}}; public int knightDialer(int n) { int[][] res = pow(base, n - 1); int ans = 0; for (int x : res[0]) { ans = (ans + x) % mod; } return ans; } private int[][] mul(int[][] a, int[][] b) { int m = a.length, n = b[0].length; int[][] c = new int[m][n]; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { for (int k = 0; k < b.length; ++k) { c[i][j] = (int) ((c[i][j] + 1L * a[i][k] * b[k][j] % mod) % mod); } } } return c; } private int[][] pow(int[][] a, int n) { int[][] res = new int[1][a.length]; Arrays.fill(res[0], 1); while (n > 0) { if ((n & 1) == 1) { res = mul(res, a); } a = mul(a, a); n >>= 1; } return res; } } -
class Solution { public: int knightDialer(int n) { const int mod = 1e9 + 7; vector<vector<int>> base = { {0, 0, 0, 0, 1, 0, 1, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 1, 0, 1, 0}, {0, 0, 0, 0, 0, 0, 0, 1, 0, 1}, {0, 0, 0, 0, 1, 0, 0, 0, 1, 0}, {1, 0, 0, 1, 0, 0, 0, 0, 0, 1}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 1, 0, 0, 0, 0, 0, 1, 0, 0}, {0, 0, 1, 0, 0, 0, 1, 0, 0, 0}, {0, 1, 0, 1, 0, 0, 0, 0, 0, 0}, {0, 0, 1, 0, 1, 0, 0, 0, 0, 0}}; vector<vector<int>> res = pow(base, n - 1, mod); return accumulate(res[0].begin(), res[0].end(), 0LL) % mod; } private: vector<vector<int>> mul(const vector<vector<int>>& a, const vector<vector<int>>& b, int mod) { int m = a.size(), n = b[0].size(); vector<vector<int>> c(m, vector<int>(n, 0)); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { for (int k = 0; k < b.size(); ++k) { c[i][j] = (c[i][j] + (1LL * a[i][k] * b[k][j]) % mod) % mod; } } } return c; } vector<vector<int>> pow(vector<vector<int>>& a, int n, int mod) { int size = a.size(); vector<vector<int>> res(1, vector<int>(size, 1)); while (n > 0) { if (n % 2 == 1) { res = mul(res, a, mod); } a = mul(a, a, mod); n /= 2; } return res; } }; -
import numpy as np base = [ (0, 0, 0, 0, 1, 0, 1, 0, 0, 0), (0, 0, 0, 0, 0, 0, 1, 0, 1, 0), (0, 0, 0, 0, 0, 0, 0, 1, 0, 1), (0, 0, 0, 0, 1, 0, 0, 0, 1, 0), (1, 0, 0, 1, 0, 0, 0, 0, 0, 1), (0, 0, 0, 0, 0, 0, 0, 0, 0, 0), (1, 1, 0, 0, 0, 0, 0, 1, 0, 0), (0, 0, 1, 0, 0, 0, 1, 0, 0, 0), (0, 1, 0, 1, 0, 0, 0, 0, 0, 0), (0, 0, 1, 0, 1, 0, 0, 0, 0, 0), ] class Solution: def knightDialer(self, n: int) -> int: factor = np.asmatrix(base, np.dtype("O")) res = np.asmatrix([[1] * 10], np.dtype("O")) n -= 1 mod = 10**9 + 7 while n: if n & 1: res = res * factor % mod factor = factor * factor % mod n >>= 1 return res.sum() % mod -
const mod = 1e9 + 7 func knightDialer(n int) int { base := [][]int{ {0, 0, 0, 0, 1, 0, 1, 0, 0, 0}, {0, 0, 0, 0, 0, 0, 1, 0, 1, 0}, {0, 0, 0, 0, 0, 0, 0, 1, 0, 1}, {0, 0, 0, 0, 1, 0, 0, 0, 1, 0}, {1, 0, 0, 1, 0, 0, 0, 0, 0, 1}, {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, {1, 1, 0, 0, 0, 0, 0, 1, 0, 0}, {0, 0, 1, 0, 0, 0, 1, 0, 0, 0}, {0, 1, 0, 1, 0, 0, 0, 0, 0, 0}, {0, 0, 1, 0, 1, 0, 0, 0, 0, 0}, } res := pow(base, n-1) ans := 0 for _, x := range res[0] { ans = (ans + x) % mod } return ans } func mul(a, b [][]int) [][]int { m := len(a) n := len(b[0]) c := make([][]int, m) for i := range c { c[i] = make([]int, n) } for i := 0; i < m; i++ { for j := 0; j < n; j++ { for k := 0; k < len(b); k++ { c[i][j] = (c[i][j] + a[i][k]*b[k][j]) % mod } } } return c } func pow(a [][]int, n int) [][]int { size := len(a) res := make([][]int, 1) res[0] = make([]int, size) for i := 0; i < size; i++ { res[0][i] = 1 } for n > 0 { if n%2 == 1 { res = mul(res, a) } a = mul(a, a) n /= 2 } return res } -
const mod = 1e9 + 7; function knightDialer(n: number): number { const base: number[][] = [ [0, 0, 0, 0, 1, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 1, 0, 1, 0], [0, 0, 0, 0, 0, 0, 0, 1, 0, 1], [0, 0, 0, 0, 1, 0, 0, 0, 1, 0], [1, 0, 0, 1, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 0, 0, 0, 0, 0, 1, 0, 0], [0, 0, 1, 0, 0, 0, 1, 0, 0, 0], [0, 1, 0, 1, 0, 0, 0, 0, 0, 0], [0, 0, 1, 0, 1, 0, 0, 0, 0, 0], ]; const res = pow(base, n - 1); let ans = 0; for (const x of res[0]) { ans = (ans + x) % mod; } return ans; } function mul(a: number[][], b: number[][]): number[][] { const m = a.length; const n = b[0].length; const c: number[][] = Array.from({ length: m }, () => Array(n).fill(0)); for (let i = 0; i < m; i++) { for (let j = 0; j < n; j++) { for (let k = 0; k < b.length; k++) { c[i][j] = (c[i][j] + Number((BigInt(a[i][k]) * BigInt(b[k][j])) % BigInt(mod))) % mod; } } } return c; } function pow(a: number[][], n: number): number[][] { const size = a.length; let res: number[][] = Array.from({ length: 1 }, () => Array(size).fill(1)); while (n > 0) { if (n % 2 === 1) { res = mul(res, a); } a = mul(a, a); n = Math.floor(n / 2); } return res; } -
public class Solution { private const int mod = 1000000007; private readonly int[][] baseMatrix = { new int[] {0, 0, 0, 0, 1, 0, 1, 0, 0, 0}, new int[] {0, 0, 0, 0, 0, 0, 1, 0, 1, 0}, new int[] {0, 0, 0, 0, 0, 0, 0, 1, 0, 1}, new int[] {0, 0, 0, 0, 1, 0, 0, 0, 1, 0}, new int[] {1, 0, 0, 1, 0, 0, 0, 0, 0, 1}, new int[] {0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, new int[] {1, 1, 0, 0, 0, 0, 0, 1, 0, 0}, new int[] {0, 0, 1, 0, 0, 0, 1, 0, 0, 0}, new int[] {0, 1, 0, 1, 0, 0, 0, 0, 0, 0}, new int[] {0, 0, 1, 0, 1, 0, 0, 0, 0, 0} }; public int KnightDialer(int n) { int[][] res = Pow(baseMatrix, n - 1); int ans = 0; foreach (var x in res[0]) { ans = (ans + x) % mod; } return ans; } private int[][] Mul(int[][] a, int[][] b) { int m = a.Length, n = b[0].Length; int[][] c = new int[m][]; for (int i = 0; i < m; i++) { c[i] = new int[n]; } for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { for (int k = 0; k < b.Length; k++) { c[i][j] = (int)((c[i][j] + (long)a[i][k] * b[k][j]) % mod); } } } return c; } private int[][] Pow(int[][] a, int n) { int size = a.Length; int[][] res = new int[1][]; res[0] = new int[size]; for (int i = 0; i < size; i++) { res[0][i] = 1; } while (n > 0) { if (n % 2 == 1) { res = Mul(res, a); } a = Mul(a, a); n /= 2; } return res; } }