Welcome to Subscribe On Youtube
913. Cat and Mouse
Description
A game on an undirected graph is played by two players, Mouse and Cat, who alternate turns.
The graph is given as follows: graph[a] is a list of all nodes b such that ab is an edge of the graph.
The mouse starts at node 1 and goes first, the cat starts at node 2 and goes second, and there is a hole at node 0.
During each player's turn, they must travel along one edge of the graph that meets where they are. For example, if the Mouse is at node 1, it must travel to any node in graph[1].
Additionally, it is not allowed for the Cat to travel to the Hole (node 0.)
Then, the game can end in three ways:
- If ever the Cat occupies the same node as the Mouse, the Cat wins.
- If ever the Mouse reaches the Hole, the Mouse wins.
- If ever a position is repeated (i.e., the players are in the same position as a previous turn, and it is the same player's turn to move), the game is a draw.
Given a graph, and assuming both players play optimally, return
1if the mouse wins the game,2if the cat wins the game, or0if the game is a draw.
Example 1:
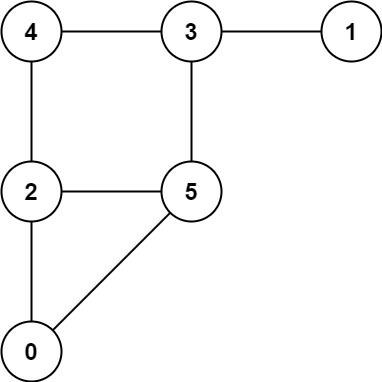
Input: graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]] Output: 0
Example 2:
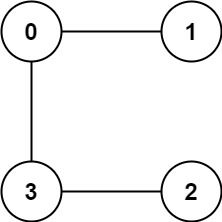
Input: graph = [[1,3],[0],[3],[0,2]] Output: 1
Constraints:
3 <= graph.length <= 501 <= graph[i].length < graph.length0 <= graph[i][j] < graph.lengthgraph[i][j] != igraph[i]is unique.- The mouse and the cat can always move.
Solutions
-
class Solution { private int n; private int[][] g; private int[][][] res; private int[][][] degree; private static final int HOLE = 0, MOUSE_START = 1, CAT_START = 2; private static final int MOUSE_TURN = 0, CAT_TURN = 1; private static final int MOUSE_WIN = 1, CAT_WIN = 2, TIE = 0; public int catMouseGame(int[][] graph) { n = graph.length; g = graph; res = new int[n][n][2]; degree = new int[n][n][2]; for (int i = 0; i < n; ++i) { for (int j = 1; j < n; ++j) { degree[i][j][MOUSE_TURN] = g[i].length; degree[i][j][CAT_TURN] = g[j].length; } } for (int i = 0; i < n; ++i) { for (int j : g[HOLE]) { --degree[i][j][CAT_TURN]; } } Deque<int[]> q = new ArrayDeque<>(); for (int j = 1; j < n; ++j) { res[0][j][MOUSE_TURN] = MOUSE_WIN; res[0][j][CAT_TURN] = MOUSE_WIN; q.offer(new int[] {0, j, MOUSE_TURN}); q.offer(new int[] {0, j, CAT_TURN}); } for (int i = 1; i < n; ++i) { res[i][i][MOUSE_TURN] = CAT_WIN; res[i][i][CAT_TURN] = CAT_WIN; q.offer(new int[] {i, i, MOUSE_TURN}); q.offer(new int[] {i, i, CAT_TURN}); } while (!q.isEmpty()) { int[] state = q.poll(); int t = res[state[0]][state[1]][state[2]]; List<int[]> prevStates = getPrevStates(state); for (var prevState : prevStates) { int pm = prevState[0], pc = prevState[1], pt = prevState[2]; if (res[pm][pc][pt] == TIE) { boolean win = (t == MOUSE_WIN && pt == MOUSE_TURN) || (t == CAT_WIN && pt == CAT_TURN); if (win) { res[pm][pc][pt] = t; q.offer(prevState); } else { if (--degree[pm][pc][pt] == 0) { res[pm][pc][pt] = t; q.offer(prevState); } } } } } return res[MOUSE_START][CAT_START][MOUSE_TURN]; } private List<int[]> getPrevStates(int[] state) { List<int[]> pre = new ArrayList<>(); int m = state[0], c = state[1], t = state[2]; int pt = t ^ 1; if (pt == CAT_TURN) { for (int pc : g[c]) { if (pc != HOLE) { pre.add(new int[] {m, pc, pt}); } } } else { for (int pm : g[m]) { pre.add(new int[] {pm, c, pt}); } } return pre; } } -
const int HOLE = 0; const int MOUSE_START = 1; const int CAT_START = 2; const int MOUSE_TURN = 0; const int CAT_TURN = 1; const int MOUSE_WIN = 1; const int CAT_WIN = 2; const int TIE = 0; class Solution { public: int catMouseGame(vector<vector<int>>& graph) { int n = graph.size(); int res[n][n][2]; int degree[n][n][2]; memset(res, 0, sizeof res); memset(degree, 0, sizeof degree); for (int i = 0; i < n; ++i) { for (int j = 1; j < n; ++j) { degree[i][j][MOUSE_TURN] = graph[i].size(); degree[i][j][CAT_TURN] = graph[j].size(); } for (int j : graph[HOLE]) { --degree[i][j][CAT_TURN]; } } auto getPrevStates = [&](int m, int c, int t) { int pt = t ^ 1; vector<tuple<int, int, int>> pre; if (pt == CAT_TURN) { for (int pc : graph[c]) { if (pc != HOLE) { pre.emplace_back(m, pc, pt); } } } else { for (int pm : graph[m]) { pre.emplace_back(pm, c, pt); } } return pre; }; queue<tuple<int, int, int>> q; for (int j = 1; j < n; ++j) { res[0][j][MOUSE_TURN] = res[0][j][CAT_TURN] = MOUSE_WIN; q.emplace(0, j, MOUSE_TURN); q.emplace(0, j, CAT_TURN); } for (int i = 1; i < n; ++i) { res[i][i][MOUSE_TURN] = res[i][i][CAT_TURN] = CAT_WIN; q.emplace(i, i, MOUSE_TURN); q.emplace(i, i, CAT_TURN); } while (!q.empty()) { auto [m, c, t] = q.front(); q.pop(); int x = res[m][c][t]; for (auto [pm, pc, pt] : getPrevStates(m, c, t)) { if (res[pm][pc][pt] == TIE) { bool win = (x == MOUSE_WIN && pt == MOUSE_TURN) || (x == CAT_WIN && pt == CAT_TURN); if (win) { res[pm][pc][pt] = x; q.emplace(pm, pc, pt); } else { if (--degree[pm][pc][pt] == 0) { res[pm][pc][pt] = x; q.emplace(pm, pc, pt); } } } } } return res[MOUSE_START][CAT_START][MOUSE_TURN]; } }; -
const ( hole = 0 mouseStart = 1 catStart = 2 mouseTurn = 0 catTurn = 1 mouseWin = 1 catWin = 2 tie = 0 ) func catMouseGame(graph [][]int) int { res := [50][50][2]int{} degree := [50][50][2]int{} n := len(graph) for i := 0; i < n; i++ { for j := 1; j < n; j++ { degree[i][j][mouseTurn] = len(graph[i]) degree[i][j][catTurn] = len(graph[j]) } for _, j := range graph[hole] { degree[i][j][catTurn]-- } } type tuple struct{ m, c, t int } q := []tuple{} for j := 1; j < n; j++ { res[0][j][mouseTurn], res[0][j][catTurn] = mouseWin, mouseWin q = append(q, tuple{0, j, mouseTurn}) q = append(q, tuple{0, j, catTurn}) } for i := 1; i < n; i++ { res[i][i][mouseTurn], res[i][i][catTurn] = catWin, catWin q = append(q, tuple{i, i, mouseTurn}) q = append(q, tuple{i, i, catTurn}) } getPrevStates := func(m, c, t int) []tuple { pre := []tuple{} pt := t ^ 1 if pt == catTurn { for _, pc := range graph[c] { if pc != hole { pre = append(pre, tuple{m, pc, pt}) } } } else { for _, pm := range graph[m] { pre = append(pre, tuple{pm, c, pt}) } } return pre } for len(q) > 0 { state := q[0] m, c, t := state.m, state.c, state.t q = q[1:] x := res[m][c][t] for _, prevState := range getPrevStates(m, c, t) { pm, pc, pt := prevState.m, prevState.c, prevState.t if res[pm][pc][pt] == tie { win := (x == mouseWin && pt == mouseTurn) || (x == catWin && pt == catTurn) if win { res[pm][pc][pt] = x q = append(q, tuple{pm, pc, pt}) } else { degree[pm][pc][pt]-- if degree[pm][pc][pt] == 0 { res[pm][pc][pt] = x q = append(q, tuple{pm, pc, pt}) } } } } } return res[mouseStart][catStart][mouseTurn] } -
HOLE, MOUSE_START, CAT_START = 0, 1, 2 MOUSE_TURN, CAT_TURN = 0, 1 MOUSE_WIN, CAT_WIN, TIE = 1, 2, 0 class Solution: def catMouseGame(self, graph: List[List[int]]) -> int: def get_prev_states(state): m, c, t = state pt = t ^ 1 pre = [] if pt == CAT_TURN: for pc in graph[c]: if pc != HOLE: pre.append((m, pc, pt)) else: for pm in graph[m]: pre.append((pm, c, pt)) return pre n = len(graph) res = [[[0, 0] for _ in range(n)] for _ in range(n)] degree = [[[0, 0] for _ in range(n)] for _ in range(n)] for i in range(n): for j in range(1, n): degree[i][j][MOUSE_TURN] = len(graph[i]) degree[i][j][CAT_TURN] = len(graph[j]) for j in graph[HOLE]: degree[i][j][CAT_TURN] -= 1 q = deque() for j in range(1, n): res[0][j][MOUSE_TURN] = res[0][j][CAT_TURN] = MOUSE_WIN q.append((0, j, MOUSE_TURN)) q.append((0, j, CAT_TURN)) for i in range(1, n): res[i][i][MOUSE_TURN] = res[i][i][CAT_TURN] = CAT_WIN q.append((i, i, MOUSE_TURN)) q.append((i, i, CAT_TURN)) while q: state = q.popleft() t = res[state[0]][state[1]][state[2]] for prev_state in get_prev_states(state): pm, pc, pt = prev_state if res[pm][pc][pt] == TIE: win = (t == MOUSE_WIN and pt == MOUSE_TURN) or ( t == CAT_WIN and pt == CAT_TURN ) if win: res[pm][pc][pt] = t q.append(prev_state) else: degree[pm][pc][pt] -= 1 if degree[pm][pc][pt] == 0: res[pm][pc][pt] = t q.append(prev_state) return res[MOUSE_START][CAT_START][MOUSE_TURN]