Welcome to Subscribe On Youtube

858. Mirror Reflection

Description

There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered 0, 1, and 2.

The square room has walls of length p and a laser ray from the southwest corner first meets the east wall at a distance q from the 0th receptor.

Given the two integers p and q, return the number of the receptor that the ray meets first.

The test cases are guaranteed so that the ray will meet a receptor eventually.

 

Example 1:

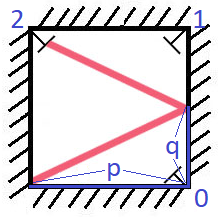
Input: p = 2, q = 1
Output: 2
Explanation: The ray meets receptor 2 the first time it gets reflected back to the left wall.

Example 2:

Input: p = 3, q = 1
Output: 1

 

Constraints:

• 1 <= q <= p <= 1000

Solutions

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      public int mirrorReflection(int p, int q) {
          int g = gcd(p, q);
          p = (p / g) % 2;
          q = (q / g) % 2;
          if (p == 1 && q == 1) {
              return 1;
          }
          return p == 1 ? 0 : 2;
      }
  
      private int gcd(int a, int b) {
          return b == 0 ? a : gcd(b, a % b);
      }
  }
  

• class Solution {
  public:
      int mirrorReflection(int p, int q) {
          int g = __gcd(p, q);
          p = (p / g) % 2;
          q = (q / g) % 2;
          if (p == 1 && q == 1) {
              return 1;
          }
          return p == 1 ? 0 : 2;
      }
  };
  

• class Solution:
      def mirrorReflection(self, p: int, q: int) -> int:
          g = gcd(p, q)
          p = (p // g) % 2
          q = (q // g) % 2
          if p == 1 and q == 1:
              return 1
          return 0 if p == 1 else 2
  
  

• func mirrorReflection(p int, q int) int {
  	g := gcd(p, q)
  	p = (p / g) % 2
  	q = (q / g) % 2
  	if p == 1 && q == 1 {
  		return 1
  	}
  	if p == 1 {
  		return 0
  	}
  	return 2
  }
  
  func gcd(a, b int) int {
  	if b == 0 {
  		return a
  	}
  	return gcd(b, a%b)
  }
  

• function mirrorReflection(p: number, q: number): number {
      const g = gcd(p, q);
      p = Math.floor(p / g) % 2;
      q = Math.floor(q / g) % 2;
      if (p === 1 && q === 1) {
          return 1;
      }
      return p === 1 ? 0 : 2;
  }
  
  function gcd(a: number, b: number): number {
      return b === 0 ? a : gcd(b, a % b);
  }
  
  

All Problems

All Solutions