Welcome to Subscribe On Youtube
840. Magic Squares In Grid
Description
A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.
Given a row x col grid of integers, how many 3 x 3 "magic square" subgrids are there? (Each subgrid is contiguous).
Example 1:
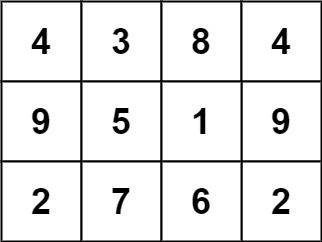
Input: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]] Output: 1 Explanation: The following subgrid is a 3 x 3 magic square:while this one is not:
In total, there is only one magic square inside the given grid.
Example 2:
Input: grid = [[8]] Output: 0
Constraints:
row == grid.lengthcol == grid[i].length1 <= row, col <= 100 <= grid[i][j] <= 15
Solutions
-
class Solution { private int m; private int n; private int[][] grid; public int numMagicSquaresInside(int[][] grid) { m = grid.length; n = grid[0].length; this.grid = grid; int ans = 0; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { ans += check(i, j); } } return ans; } private int check(int i, int j) { if (i + 3 > m || j + 3 > n) { return 0; } int[] cnt = new int[16]; int[] row = new int[3]; int[] col = new int[3]; int a = 0, b = 0; for (int x = i; x < i + 3; ++x) { for (int y = j; y < j + 3; ++y) { int v = grid[x][y]; if (v < 1 || v > 9 || ++cnt[v] > 1) { return 0; } row[x - i] += v; col[y - j] += v; if (x - i == y - j) { a += v; } if (x - i + y - j == 2) { b += v; } } } if (a != b) { return 0; } for (int k = 0; k < 3; ++k) { if (row[k] != a || col[k] != a) { return 0; } } return 1; } } -
class Solution { public: int numMagicSquaresInside(vector<vector<int>>& grid) { int m = grid.size(); int n = grid[0].size(); int ans = 0; auto check = [&](int i, int j) { if (i + 3 > m || j + 3 > n) { return 0; } vector<int> cnt(16); vector<int> row(3); vector<int> col(3); int a = 0, b = 0; for (int x = i; x < i + 3; ++x) { for (int y = j; y < j + 3; ++y) { int v = grid[x][y]; if (v < 1 || v > 9 || ++cnt[v] > 1) { return 0; } row[x - i] += v; col[y - j] += v; if (x - i == y - j) { a += v; } if (x - i + y - j == 2) { b += v; } } } if (a != b) { return 0; } for (int k = 0; k < 3; ++k) { if (row[k] != a || col[k] != a) { return 0; } } return 1; }; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { ans += check(i, j); } } return ans; } }; -
class Solution: def numMagicSquaresInside(self, grid: List[List[int]]) -> int: def check(i: int, j: int) -> int: if i + 3 > m or j + 3 > n: return 0 s = set() row = [0] * 3 col = [0] * 3 a = b = 0 for x in range(i, i + 3): for y in range(j, j + 3): v = grid[x][y] if v < 1 or v > 9: return 0 s.add(v) row[x - i] += v col[y - j] += v if x - i == y - j: a += v if x - i == 2 - (y - j): b += v if len(s) != 9 or a != b: return 0 if any(x != a for x in row) or any(x != a for x in col): return 0 return 1 m, n = len(grid), len(grid[0]) return sum(check(i, j) for i in range(m) for j in range(n)) -
func numMagicSquaresInside(grid [][]int) (ans int) { m, n := len(grid), len(grid[0]) check := func(i, j int) int { if i+3 > m || j+3 > n { return 0 } cnt := [16]int{} row := [3]int{} col := [3]int{} a, b := 0, 0 for x := i; x < i+3; x++ { for y := j; y < j+3; y++ { v := grid[x][y] if v < 1 || v > 9 || cnt[v] > 0 { return 0 } cnt[v]++ row[x-i] += v col[y-j] += v if x-i == y-j { a += v } if x-i == 2-(y-j) { b += v } } } if a != b { return 0 } for k := 0; k < 3; k++ { if row[k] != a || col[k] != a { return 0 } } return 1 } for i := 0; i < m; i++ { for j := 0; j < n; j++ { ans += check(i, j) } } return } -
function numMagicSquaresInside(grid: number[][]): number { const m = grid.length; const n = grid[0].length; const check = (i: number, j: number): number => { if (i + 3 > m || j + 3 > n) { return 0; } const cnt: number[] = new Array(16).fill(0); const row: number[] = new Array(3).fill(0); const col: number[] = new Array(3).fill(0); let [a, b] = [0, 0]; for (let x = i; x < i + 3; ++x) { for (let y = j; y < j + 3; ++y) { const v = grid[x][y]; if (v < 1 || v > 9 || ++cnt[v] > 1) { return 0; } row[x - i] += v; col[y - j] += v; if (x - i === y - j) { a += v; } if (x - i === 2 - (y - j)) { b += v; } } } if (a !== b) { return 0; } for (let k = 0; k < 3; ++k) { if (row[k] !== a || col[k] !== a) { return 0; } } return 1; }; let ans = 0; for (let i = 0; i < m; ++i) { for (let j = 0; j < n; ++j) { ans += check(i, j); } } return ans; }