Welcome to Subscribe On Youtube

812. Largest Triangle Area

Description

Given an array of points on the X-Y plane points where points[i] = [xi, yi], return the area of the largest triangle that can be formed by any three different points. Answers within 10-5 of the actual answer will be accepted.

 

Example 1:

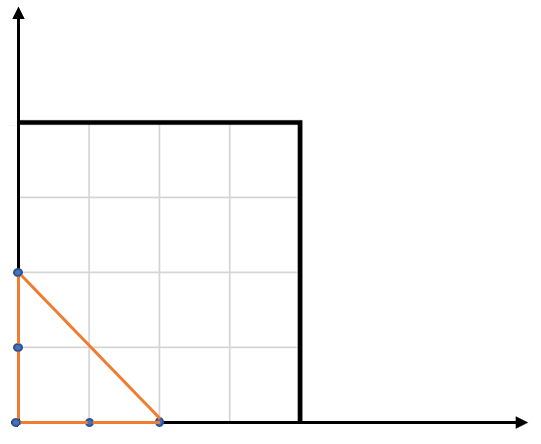
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2.00000
Explanation: The five points are shown in the above figure. The red triangle is the largest.

Example 2:

Input: points = [[1,0],[0,0],[0,1]]
Output: 0.50000

 

Constraints:

• 3 <= points.length <= 50
• -50 <= xi, yi <= 50
• All the given points are unique.

Solutions

• Java
• C++
• Python
• Go

• class Solution {
      public double largestTriangleArea(int[][] points) {
          double ans = 0;
          for (int[] p1 : points) {
              int x1 = p1[0], y1 = p1[1];
              for (int[] p2 : points) {
                  int x2 = p2[0], y2 = p2[1];
                  for (int[] p3 : points) {
                      int x3 = p3[0], y3 = p3[1];
                      int u1 = x2 - x1, v1 = y2 - y1;
                      int u2 = x3 - x1, v2 = y3 - y1;
                      double t = Math.abs(u1 * v2 - u2 * v1) / 2.0;
                      ans = Math.max(ans, t);
                  }
              }
          }
          return ans;
      }
  }
  

• class Solution {
  public:
      double largestTriangleArea(vector<vector<int>>& points) {
          double ans = 0;
          for (auto& p1 : points) {
              int x1 = p1[0], y1 = p1[1];
              for (auto& p2 : points) {
                  int x2 = p2[0], y2 = p2[1];
                  for (auto& p3 : points) {
                      int x3 = p3[0], y3 = p3[1];
                      int u1 = x2 - x1, v1 = y2 - y1;
                      int u2 = x3 - x1, v2 = y3 - y1;
                      double t = abs(u1 * v2 - u2 * v1) / 2.0;
                      ans = max(ans, t);
                  }
              }
          }
          return ans;
      }
  };
  

• class Solution:
      def largestTriangleArea(self, points: List[List[int]]) -> float:
          ans = 0
          for x1, y1 in points:
              for x2, y2 in points:
                  for x3, y3 in points:
                      u1, v1 = x2 - x1, y2 - y1
                      u2, v2 = x3 - x1, y3 - y1
                      t = abs(u1 * v2 - u2 * v1) / 2
                      ans = max(ans, t)
          return ans
  
  

• func largestTriangleArea(points [][]int) float64 {
  	ans := 0.0
  	for _, p1 := range points {
  		x1, y1 := p1[0], p1[1]
  		for _, p2 := range points {
  			x2, y2 := p2[0], p2[1]
  			for _, p3 := range points {
  				x3, y3 := p3[0], p3[1]
  				u1, v1 := x2-x1, y2-y1
  				u2, v2 := x3-x1, y3-y1
  				t := float64(abs(u1*v2-u2*v1)) / 2.0
  				ans = math.Max(ans, t)
  			}
  		}
  	}
  	return ans
  }
  
  func abs(x int) int {
  	if x < 0 {
  		return -x
  	}
  	return x
  }
  

All Problems

All Solutions