Welcome to Subscribe On Youtube

790. Domino and Tromino Tiling

Description

You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.

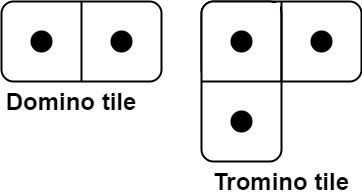
Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 109 + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

 

Example 1:

Input: n = 3
Output: 5
Explanation: The five different ways are show above.

Example 2:

Input: n = 1
Output: 1

 

Constraints:

• 1 <= n <= 1000

Solutions

• Java
• C++
• Python
• Go

• class Solution {
      public int numTilings(int n) {
          long[] f = {1, 0, 0, 0};
          int mod = (int) 1e9 + 7;
          for (int i = 1; i <= n; ++i) {
              long[] g = new long[4];
              g[0] = (f[0] + f[1] + f[2] + f[3]) % mod;
              g[1] = (f[2] + f[3]) % mod;
              g[2] = (f[1] + f[3]) % mod;
              g[3] = f[0];
              f = g;
          }
          return (int) f[0];
      }
  }
  

• class Solution {
  public:
      const int mod = 1e9 + 7;
  
      int numTilings(int n) {
          long f[4] = {1, 0, 0, 0};
          for (int i = 1; i <= n; ++i) {
              long g[4] = {0, 0, 0, 0};
              g[0] = (f[0] + f[1] + f[2] + f[3]) % mod;
              g[1] = (f[2] + f[3]) % mod;
              g[2] = (f[1] + f[3]) % mod;
              g[3] = f[0];
              memcpy(f, g, sizeof(g));
          }
          return f[0];
      }
  };
  

• class Solution:
      def numTilings(self, n: int) -> int:
          @cache
          def dfs(i, j):
              if i > n or j > n:
                  return 0
              if i == n and j == n:
                  return 1
              ans = 0
              if i == j:
                  ans = (
                      dfs(i + 2, j + 2)
                      + dfs(i + 1, j + 1)
                      + dfs(i + 2, j + 1)
                      + dfs(i + 1, j + 2)
                  )
              elif i > j:
                  ans = dfs(i, j + 2) + dfs(i + 1, j + 2)
              else:
                  ans = dfs(i + 2, j) + dfs(i + 2, j + 1)
              return ans % mod
  
          mod = 10**9 + 7
          return dfs(0, 0)
  
  

• func numTilings(n int) int {
  	f := [4]int{}
  	f[0] = 1
  	const mod int = 1e9 + 7
  	for i := 1; i <= n; i++ {
  		g := [4]int{}
  		g[0] = (f[0] + f[1] + f[2] + f[3]) % mod
  		g[1] = (f[2] + f[3]) % mod
  		g[2] = (f[1] + f[3]) % mod
  		g[3] = f[0]
  		f = g
  	}
  	return f[0]
  }
  

All Problems

All Solutions