Welcome to Subscribe On Youtube

756. Pyramid Transition Matrix

Description

You are stacking blocks to form a pyramid. Each block has a color, which is represented by a single letter. Each row of blocks contains one less block than the row beneath it and is centered on top.

To make the pyramid aesthetically pleasing, there are only specific triangular patterns that are allowed. A triangular pattern consists of a single block stacked on top of two blocks. The patterns are given as a list of three-letter strings allowed, where the first two characters of a pattern represent the left and right bottom blocks respectively, and the third character is the top block.

• For example, "ABC" represents a triangular pattern with a 'C' block stacked on top of an 'A' (left) and 'B' (right) block. Note that this is different from "BAC" where 'B' is on the left bottom and 'A' is on the right bottom.

You start with a bottom row of blocks bottom, given as a single string, that you must use as the base of the pyramid.

Given bottom and allowed, return true if you can build the pyramid all the way to the top such that every triangular pattern in the pyramid is in allowed, or false otherwise.

 

Example 1:

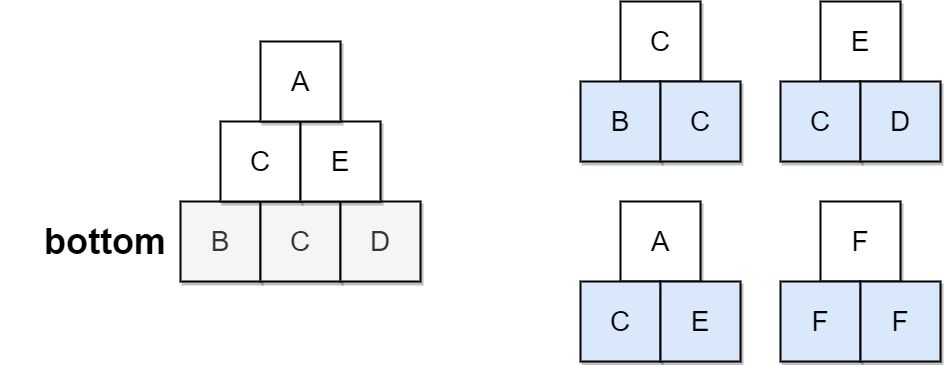
Input: bottom = "BCD", allowed = ["BCC","CDE","CEA","FFF"]
Output: true
Explanation: The allowed triangular patterns are shown on the right.
Starting from the bottom (level 3), we can build "CE" on level 2 and then build "A" on level 1.
There are three triangular patterns in the pyramid, which are "BCC", "CDE", and "CEA". All are allowed.

Example 2:

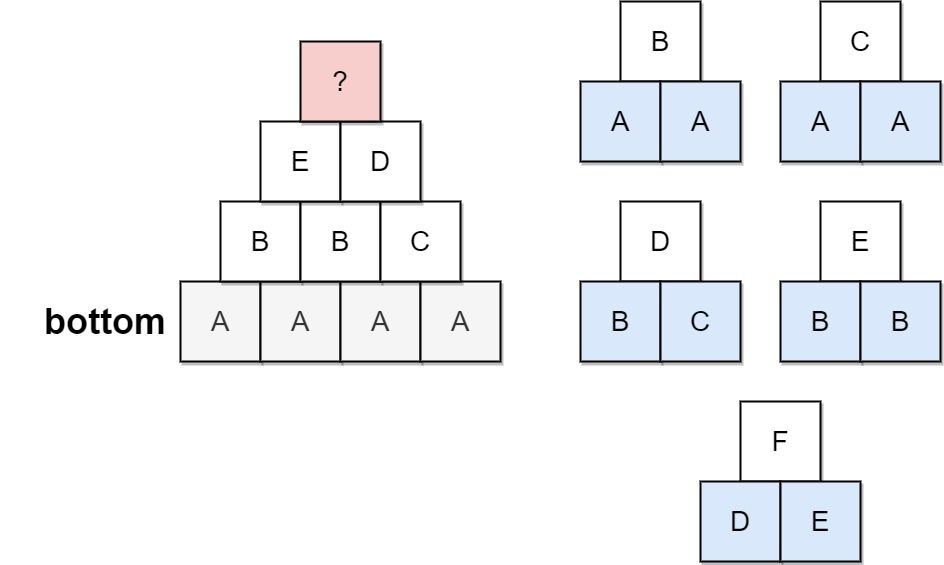
Input: bottom = "AAAA", allowed = ["AAB","AAC","BCD","BBE","DEF"]
Output: false
Explanation: The allowed triangular patterns are shown on the right.
Starting from the bottom (level 4), there are multiple ways to build level 3, but trying all the possibilites, you will get always stuck before building level 1.

 

Constraints:

• 2 <= bottom.length <= 6
• 0 <= allowed.length <= 216
• allowed[i].length == 3
• The letters in all input strings are from the set {'A', 'B', 'C', 'D', 'E', 'F'}.
• All the values of allowed are unique.

Solutions

• Java
• C++
• Python
• Go

• class Solution {
      private int[][] f = new int[7][7];
      private Map<String, Boolean> dp = new HashMap<>();
  
      public boolean pyramidTransition(String bottom, List<String> allowed) {
          for (String s : allowed) {
              int a = s.charAt(0) - 'A', b = s.charAt(1) - 'A';
              f[a][b] |= 1 << (s.charAt(2) - 'A');
          }
          return dfs(bottom, new StringBuilder());
      }
  
      boolean dfs(String s, StringBuilder t) {
          if (s.length() == 1) {
              return true;
          }
          if (t.length() + 1 == s.length()) {
              return dfs(t.toString(), new StringBuilder());
          }
          String k = s + "." + t.toString();
          if (dp.containsKey(k)) {
              return dp.get(k);
          }
          int a = s.charAt(t.length()) - 'A', b = s.charAt(t.length() + 1) - 'A';
          int cs = f[a][b];
          for (int i = 0; i < 7; ++i) {
              if (((cs >> i) & 1) == 1) {
                  t.append((char) ('A' + i));
                  if (dfs(s, t)) {
                      dp.put(k, true);
                      return true;
                  }
                  t.deleteCharAt(t.length() - 1);
              }
          }
          dp.put(k, false);
          return false;
      }
  }
  

• class Solution {
  public:
      int f[7][7];
      unordered_map<string, bool> dp;
  
      bool pyramidTransition(string bottom, vector<string>& allowed) {
          memset(f, 0, sizeof f);
          for (auto& s : allowed) {
              int a = s[0] - 'A', b = s[1] - 'A';
              f[a][b] |= 1 << (s[2] - 'A');
          }
          return dfs(bottom, "");
      }
  
      bool dfs(string& s, string t) {
          if (s.size() == 1) {
              return true;
          }
          if (t.size() + 1 == s.size()) {
              return dfs(t, "");
          }
          string k = s + "." + t;
          if (dp.count(k)) {
              return dp[k];
          }
          int a = s[t.size()] - 'A', b = s[t.size() + 1] - 'A';
          int cs = f[a][b];
          for (int i = 0; i < 7; ++i) {
              if ((cs >> i) & 1) {
                  if (dfs(s, t + (char) (i + 'A'))) {
                      dp[k] = true;
                      return true;
                  }
              }
          }
          dp[k] = false;
          return false;
      }
  };
  

• class Solution:
      def pyramidTransition(self, bottom: str, allowed: List[str]) -> bool:
          @cache
          def dfs(s):
              if len(s) == 1:
                  return True
              t = []
              for a, b in pairwise(s):
                  cs = d[a, b]
                  if not cs:
                      return False
                  t.append(cs)
              return any(dfs(''.join(nxt)) for nxt in product(*t))
  
          d = defaultdict(list)
          for a, b, c in allowed:
              d[a, b].append(c)
          return dfs(bottom)
  
  

• func pyramidTransition(bottom string, allowed []string) bool {
  	f := make([][]int, 7)
  	for i := range f {
  		f[i] = make([]int, 7)
  	}
  	for _, s := range allowed {
  		a, b := s[0]-'A', s[1]-'A'
  		f[a][b] |= 1 << (s[2] - 'A')
  	}
  	dp := map[string]bool{}
  	var dfs func(s string, t []byte) bool
  	dfs = func(s string, t []byte) bool {
  		if len(s) == 1 {
  			return true
  		}
  		if len(t)+1 == len(s) {
  			return dfs(string(t), []byte{})
  		}
  		k := s + "." + string(t)
  		if v, ok := dp[k]; ok {
  			return v
  		}
  		a, b := s[len(t)]-'A', s[len(t)+1]-'A'
  		cs := f[a][b]
  		for i := 0; i < 7; i++ {
  			if ((cs >> i) & 1) == 1 {
  				t = append(t, byte('A'+i))
  				if dfs(s, t) {
  					dp[k] = true
  					return true
  				}
  				t = t[:len(t)-1]
  			}
  		}
  		dp[k] = false
  		return false
  	}
  	return dfs(bottom, []byte{})
  }
  

All Problems

All Solutions