Welcome to Subscribe On Youtube
741. Cherry Pickup
Description
You are given an n x n grid representing a field of cherries, each cell is one of three possible integers.
0means the cell is empty, so you can pass through,1means the cell contains a cherry that you can pick up and pass through, or-1means the cell contains a thorn that blocks your way.
Return the maximum number of cherries you can collect by following the rules below:
- Starting at the position
(0, 0)and reaching(n - 1, n - 1)by moving right or down through valid path cells (cells with value0or1). - After reaching
(n - 1, n - 1), returning to(0, 0)by moving left or up through valid path cells. - When passing through a path cell containing a cherry, you pick it up, and the cell becomes an empty cell
0. - If there is no valid path between
(0, 0)and(n - 1, n - 1), then no cherries can be collected.
Example 1:
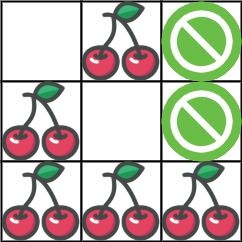
Input: grid = [[0,1,-1],[1,0,-1],[1,1,1]] Output: 5 Explanation: The player started at (0, 0) and went down, down, right right to reach (2, 2). 4 cherries were picked up during this single trip, and the matrix becomes [[0,1,-1],[0,0,-1],[0,0,0]]. Then, the player went left, up, up, left to return home, picking up one more cherry. The total number of cherries picked up is 5, and this is the maximum possible.
Example 2:
Input: grid = [[1,1,-1],[1,-1,1],[-1,1,1]] Output: 0
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 50grid[i][j]is-1,0, or1.grid[0][0] != -1grid[n - 1][n - 1] != -1
Solutions
Dynamic programming.
-
class Solution { public int cherryPickup(int[][] grid) { int n = grid.length; int[][][] dp = new int[n * 2][n][n]; dp[0][0][0] = grid[0][0]; for (int k = 1; k < n * 2 - 1; ++k) { for (int i1 = 0; i1 < n; ++i1) { for (int i2 = 0; i2 < n; ++i2) { int j1 = k - i1, j2 = k - i2; dp[k][i1][i2] = Integer.MIN_VALUE; if (j1 < 0 || j1 >= n || j2 < 0 || j2 >= n || grid[i1][j1] == -1 || grid[i2][j2] == -1) { continue; } int t = grid[i1][j1]; if (i1 != i2) { t += grid[i2][j2]; } for (int x1 = i1 - 1; x1 <= i1; ++x1) { for (int x2 = i2 - 1; x2 <= i2; ++x2) { if (x1 >= 0 && x2 >= 0) { dp[k][i1][i2] = Math.max(dp[k][i1][i2], dp[k - 1][x1][x2] + t); } } } } } } return Math.max(0, dp[n * 2 - 2][n - 1][n - 1]); } } -
class Solution { public: int cherryPickup(vector<vector<int>>& grid) { int n = grid.size(); vector<vector<vector<int>>> dp(n << 1, vector<vector<int>>(n, vector<int>(n, -1e9))); dp[0][0][0] = grid[0][0]; for (int k = 1; k < n * 2 - 1; ++k) { for (int i1 = 0; i1 < n; ++i1) { for (int i2 = 0; i2 < n; ++i2) { int j1 = k - i1, j2 = k - i2; if (j1 < 0 || j1 >= n || j2 < 0 || j2 >= n || grid[i1][j1] == -1 || grid[i2][j2] == -1) continue; int t = grid[i1][j1]; if (i1 != i2) t += grid[i2][j2]; for (int x1 = i1 - 1; x1 <= i1; ++x1) for (int x2 = i2 - 1; x2 <= i2; ++x2) if (x1 >= 0 && x2 >= 0) dp[k][i1][i2] = max(dp[k][i1][i2], dp[k - 1][x1][x2] + t); } } } return max(0, dp[n * 2 - 2][n - 1][n - 1]); } }; -
class Solution: def cherryPickup(self, grid: List[List[int]]) -> int: n = len(grid) dp = [[[-inf] * n for _ in range(n)] for _ in range((n << 1) - 1)] dp[0][0][0] = grid[0][0] for k in range(1, (n << 1) - 1): for i1 in range(n): for i2 in range(n): j1, j2 = k - i1, k - i2 if ( not 0 <= j1 < n or not 0 <= j2 < n or grid[i1][j1] == -1 or grid[i2][j2] == -1 ): continue t = grid[i1][j1] if i1 != i2: t += grid[i2][j2] for x1 in range(i1 - 1, i1 + 1): for x2 in range(i2 - 1, i2 + 1): if x1 >= 0 and x2 >= 0: dp[k][i1][i2] = max( dp[k][i1][i2], dp[k - 1][x1][x2] + t ) return max(0, dp[-1][-1][-1]) -
func cherryPickup(grid [][]int) int { n := len(grid) dp := make([][][]int, (n<<1)-1) for i := range dp { dp[i] = make([][]int, n) for j := range dp[i] { dp[i][j] = make([]int, n) } } dp[0][0][0] = grid[0][0] for k := 1; k < (n<<1)-1; k++ { for i1 := 0; i1 < n; i1++ { for i2 := 0; i2 < n; i2++ { dp[k][i1][i2] = int(-1e9) j1, j2 := k-i1, k-i2 if j1 < 0 || j1 >= n || j2 < 0 || j2 >= n || grid[i1][j1] == -1 || grid[i2][j2] == -1 { continue } t := grid[i1][j1] if i1 != i2 { t += grid[i2][j2] } for x1 := i1 - 1; x1 <= i1; x1++ { for x2 := i2 - 1; x2 <= i2; x2++ { if x1 >= 0 && x2 >= 0 { dp[k][i1][i2] = max(dp[k][i1][i2], dp[k-1][x1][x2]+t) } } } } } } return max(0, dp[n*2-2][n-1][n-1]) } -
/** * @param {number[][]} grid * @return {number} */ var cherryPickup = function (grid) { const n = grid.length; let dp = new Array(n * 2 - 1); for (let k = 0; k < dp.length; ++k) { dp[k] = new Array(n); for (let i = 0; i < n; ++i) { dp[k][i] = new Array(n).fill(-1e9); } } dp[0][0][0] = grid[0][0]; for (let k = 1; k < n * 2 - 1; ++k) { for (let i1 = 0; i1 < n; ++i1) { for (let i2 = 0; i2 < n; ++i2) { const j1 = k - i1, j2 = k - i2; if ( j1 < 0 || j1 >= n || j2 < 0 || j2 >= n || grid[i1][j1] == -1 || grid[i2][j2] == -1 ) { continue; } let t = grid[i1][j1]; if (i1 != i2) { t += grid[i2][j2]; } for (let x1 = i1 - 1; x1 <= i1; ++x1) { for (let x2 = i2 - 1; x2 <= i2; ++x2) { if (x1 >= 0 && x2 >= 0) { dp[k][i1][i2] = Math.max(dp[k][i1][i2], dp[k - 1][x1][x2] + t); } } } } } } return Math.max(0, dp[n * 2 - 2][n - 1][n - 1]); }; -
function cherryPickup(grid: number[][]): number { const n: number = grid.length; const f: number[][][] = Array.from({ length: n * 2 - 1 }, () => Array.from({ length: n }, () => Array.from({ length: n }, () => -Infinity)), ); f[0][0][0] = grid[0][0]; for (let k = 1; k < n * 2 - 1; ++k) { for (let i1 = 0; i1 < n; ++i1) { for (let i2 = 0; i2 < n; ++i2) { const [j1, j2]: [number, number] = [k - i1, k - i2]; if ( j1 < 0 || j1 >= n || j2 < 0 || j2 >= n || grid[i1][j1] == -1 || grid[i2][j2] == -1 ) { continue; } const t: number = grid[i1][j1] + (i1 != i2 ? grid[i2][j2] : 0); for (let x1 = i1 - 1; x1 <= i1; ++x1) { for (let x2 = i2 - 1; x2 <= i2; ++x2) { if (x1 >= 0 && x2 >= 0) { f[k][i1][i2] = Math.max(f[k][i1][i2], f[k - 1][x1][x2] + t); } } } } } } return Math.max(0, f[n * 2 - 2][n - 1][n - 1]); }