Welcome to Subscribe On Youtube
675. Cut Off Trees for Golf Event
Description
You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an m x n matrix. In this matrix:
0means the cell cannot be walked through.1represents an empty cell that can be walked through.- A number greater than
1represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes 1 (an empty cell).
Starting from the point (0, 0), return the minimum steps you need to walk to cut off all the trees. If you cannot cut off all the trees, return -1.
Note: The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
Example 1:
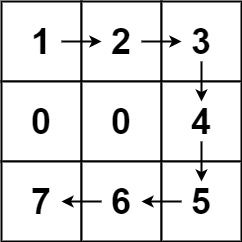
Input: forest = [[1,2,3],[0,0,4],[7,6,5]] Output: 6 Explanation: Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
Example 2:
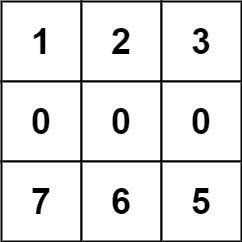
Input: forest = [[1,2,3],[0,0,0],[7,6,5]] Output: -1 Explanation: The trees in the bottom row cannot be accessed as the middle row is blocked.
Example 3:
Input: forest = [[2,3,4],[0,0,5],[8,7,6]] Output: 6 Explanation: You can follow the same path as Example 1 to cut off all the trees. Note that you can cut off the first tree at (0, 0) before making any steps.
Constraints:
m == forest.lengthn == forest[i].length1 <= m, n <= 500 <= forest[i][j] <= 109- Heights of all trees are distinct.
Solutions
-
class Solution { private int[] dist = new int[3600]; private List<List<Integer>> forest; private int m; private int n; public int cutOffTree(List<List<Integer>> forest) { this.forest = forest; m = forest.size(); n = forest.get(0).size(); List<int[]> trees = new ArrayList<>(); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (forest.get(i).get(j) > 1) { trees.add(new int[] {forest.get(i).get(j), i * n + j}); } } } trees.sort(Comparator.comparingInt(a -> a[0])); int ans = 0; int start = 0; for (int[] tree : trees) { int end = tree[1]; int t = bfs(start, end); if (t == -1) { return -1; } ans += t; start = end; } return ans; } private int bfs(int start, int end) { PriorityQueue<int[]> q = new PriorityQueue<>(Comparator.comparingInt(a -> a[0])); q.offer(new int[] {f(start, end), start}); Arrays.fill(dist, Integer.MAX_VALUE); dist[start] = 0; int[] dirs = {-1, 0, 1, 0, -1}; while (!q.isEmpty()) { int state = q.poll()[1]; if (state == end) { return dist[state]; } for (int k = 0; k < 4; ++k) { int x = state / n + dirs[k]; int y = state % n + dirs[k + 1]; if (x >= 0 && x < m && y >= 0 && y < n && forest.get(x).get(y) > 0) { if (dist[x * n + y] > dist[state] + 1) { dist[x * n + y] = dist[state] + 1; q.offer(new int[] {dist[x * n + y] + f(x * n + y, end), x * n + y}); } } } } return -1; } private int f(int start, int end) { int a = start / n; int b = start % n; int c = end / n; int d = end % n; return Math.abs(a - c) + Math.abs(b - d); } } -
class Solution { public: int m; int n; vector<int> dist; int cutOffTree(vector<vector<int>>& forest) { m = forest.size(); n = forest[0].size(); dist.resize(3600); vector<pair<int, int>> trees; for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) if (forest[i][j] > 1) trees.push_back({forest[i][j], i * n + j}); sort(trees.begin(), trees.end()); int ans = 0; int start = 0; for (auto& tree : trees) { int end = tree.second; int t = bfs(start, end, forest); if (t == -1) return -1; ans += t; start = end; } return ans; } int bfs(int start, int end, vector<vector<int>>& forest) { priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q; q.push({f(start, end), start}); fill(dist.begin(), dist.end(), INT_MAX); dist[start] = 0; vector<int> dirs = {-1, 0, 1, 0, -1}; while (!q.empty()) { int state = q.top().second; q.pop(); if (state == end) return dist[state]; for (int k = 0; k < 4; ++k) { int x = state / n + dirs[k], y = state % n + dirs[k + 1]; if (x >= 0 && x < m && y >= 0 && y < n && forest[x][y] && dist[x * n + y] > dist[state] + 1) { dist[x * n + y] = dist[state] + 1; q.push({dist[x * n + y] + f(x * n + y, end), x * n + y}); } } } return -1; } int f(int start, int end) { int a = start / n, b = start % n; int c = end / n, d = end % n; return abs(a - c) + abs(b - d); } }; -
class Solution: def cutOffTree(self, forest: List[List[int]]) -> int: def f(i, j, x, y): return abs(i - x) + abs(j - y) def bfs(i, j, x, y): q = [(f(i, j, x, y), i, j)] dist = {i * n + j: 0} while q: _, i, j = heappop(q) step = dist[i * n + j] if (i, j) == (x, y): return step for a, b in [[0, -1], [0, 1], [-1, 0], [1, 0]]: c, d = i + a, j + b if 0 <= c < m and 0 <= d < n and forest[c][d] > 0: if c * n + d not in dist or dist[c * n + d] > step + 1: dist[c * n + d] = step + 1 heappush(q, (dist[c * n + d] + f(c, d, x, y), c, d)) return -1 m, n = len(forest), len(forest[0]) trees = [ (forest[i][j], i, j) for i in range(m) for j in range(n) if forest[i][j] > 1 ] trees.sort() i = j = 0 ans = 0 for _, x, y in trees: t = bfs(i, j, x, y) if t == -1: return -1 ans += t i, j = x, y return ans -
var dirs = [][]int{ {-1, 0}, {1, 0}, {0, -1}, {0, 1} } type tree struct { height int pos int } func cutOffTree(forest [][]int) int { row, col := len(forest), len(forest[0]) bfs := func(start, end int) int { q := []int{start} vis := make(map[int]bool) vis[start] = true step := 0 for n := len(q); n > 0; n = len(q) { for i := 0; i < n; i++ { state := q[0] q = q[1:] if state == end { return step } for k := 0; k < 4; k++ { x, y := state/col+dirs[k][0], state%col+dirs[k][1] nxt := x*col + y if x >= 0 && x < row && y >= 0 && y < col && forest[x][y] != 0 && !vis[nxt] { q = append(q, nxt) vis[nxt] = true } } } step++ } return -1 } var trees []tree for i := 0; i < row; i++ { for j := 0; j < col; j++ { if forest[i][j] > 1 { trees = append(trees, tree{forest[i][j], i*col + j}) } } } sort.Slice(trees, func(i, j int) bool { return trees[i].height < trees[j].height }) ans, start := 0, 0 for _, t := range trees { end := t.pos step := bfs(start, end) if step == -1 { return -1 } ans += step start = end } return ans } -
use std::collections::HashSet; use std::collections::VecDeque; const DIRS: [[i32; 2]; 4] = [ [-1, 0], [1, 0], [0, -1], [0, 1], ]; impl Solution { pub fn cut_off_tree(forest: Vec<Vec<i32>>) -> i32 { let (row, col) = (forest.len() as i32, forest[0].len() as i32); let bfs = |start: i32, end: i32| -> i32 { let mut queue = VecDeque::new(); let mut vis = HashSet::new(); queue.push_back(start); vis.insert(start); let mut step = 0; while !queue.is_empty() { let n = queue.len(); for _ in 0..n { let state = queue.pop_front().unwrap(); if state == end { return step; } for k in 0..4 { let x = state / col + DIRS[k][0]; let y = (state % col) + DIRS[k][1]; let nxt = x * col + y; if x >= 0 && x < row && y >= 0 && y < col && forest[x as usize][y as usize] != 0 && !vis.contains(&nxt) { queue.push_back(nxt); vis.insert(nxt); } } } step += 1; } -1 }; let mut trees = Vec::new(); for i in 0..row { for j in 0..col { let height = forest[i as usize][j as usize]; if height > 1 { trees.push((height, i * col + j)); } } } trees.sort(); let (mut ans, mut start) = (0, 0); for t in &trees { let end = t.1; let step = bfs(start, end); if step == -1 { return -1; } ans += step; start = end; } ans } }