Welcome to Subscribe On Youtube
633. Sum of Square Numbers
Description
Given a non-negative integer c, decide whether there're two integers a and b such that a2 + b2 = c.
Example 1:
Input: c = 5 Output: true Explanation: 1 * 1 + 2 * 2 = 5
Example 2:
Input: c = 3 Output: false
Constraints:
0 <= c <= 231 - 1
Solutions
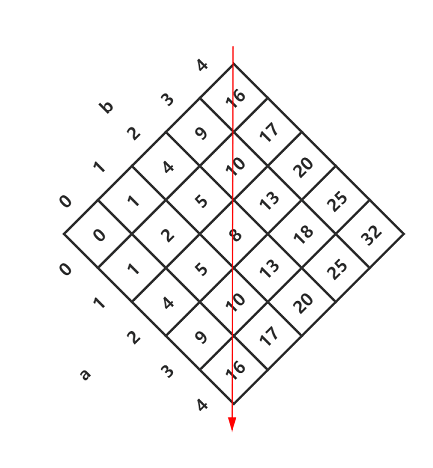
The picture above shows the relationship between a, b, and c. This question is actually looking up c in this table
From the upper right corner of the table, it is not difficult to find that it is similar to a binary search tree, so just start from the upper right corner and search according to the law of the binary search tree
-
class Solution { public boolean judgeSquareSum(int c) { long a = 0, b = (long) Math.sqrt(c); while (a <= b) { long s = a * a + b * b; if (s == c) { return true; } if (s < c) { ++a; } else { --b; } } return false; } } -
class Solution { public: bool judgeSquareSum(int c) { long a = 0, b = (long) sqrt(c); while (a <= b) { long s = a * a + b * b; if (s == c) return true; if (s < c) ++a; else --b; } return false; } }; -
class Solution: def judgeSquareSum(self, c: int) -> bool: a, b = 0, int(sqrt(c)) while a <= b: s = a**2 + b**2 if s == c: return True if s < c: a += 1 else: b -= 1 return False -
func judgeSquareSum(c int) bool { a, b := 0, int(math.Sqrt(float64(c))) for a <= b { s := a*a + b*b if s == c { return true } if s < c { a++ } else { b-- } } return false } -
function judgeSquareSum(c: number): boolean { let a = 0, b = Math.floor(Math.sqrt(c)); while (a <= b) { let sum = a ** 2 + b ** 2; if (sum == c) return true; if (sum < c) { ++a; } else { --b; } } return false; } -
use std::cmp::Ordering; impl Solution { pub fn judge_square_sum(c: i32) -> bool { let c = c as i64; let mut left = 0; let mut right = (c as f64).sqrt() as i64; while left <= right { let num = left * left + right * right; match num.cmp(&c) { Ordering::Less => { left += 1; } Ordering::Greater => { right -= 1; } Ordering::Equal => { return true; } } } false } }