Welcome to Subscribe On Youtube

598. Range Addition II

Description

You are given an m x n matrix M initialized with all 0's and an array of operations ops, where ops[i] = [ai, bi] means M[x][y] should be incremented by one for all 0 <= x < ai and 0 <= y < bi.

Count and return the number of maximum integers in the matrix after performing all the operations.

 

Example 1:

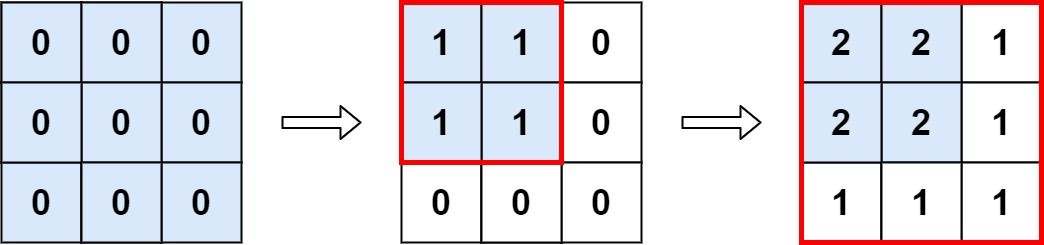
Input: m = 3, n = 3, ops = [[2,2],[3,3]]
Output: 4
Explanation: The maximum integer in M is 2, and there are four of it in M. So return 4.

Example 2:

Input: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
Output: 4

Example 3:

Input: m = 3, n = 3, ops = []
Output: 9

 

Constraints:

• 1 <= m, n <= 4 * 104
• 0 <= ops.length <= 104
• ops[i].length == 2
• 1 <= ai <= m
• 1 <= bi <= n

Solutions

Since each operation adds all the elements in the top left corner by one (according to the given row and the given column in each operation), simply obtain the minimum row r and the minimum column c among all the given operations, and the number of maximum integers in the matrix is r * c.

• Java
• C++
• Python
• Go
• TypeScript
• Javascript
• RenderScript

• class Solution {
      public int maxCount(int m, int n, int[][] ops) {
          for (int[] op : ops) {
              m = Math.min(m, op[0]);
              n = Math.min(n, op[1]);
          }
          return m * n;
      }
  }
  

• class Solution {
  public:
      int maxCount(int m, int n, vector<vector<int>>& ops) {
          for (auto op : ops) {
              m = min(m, op[0]);
              n = min(n, op[1]);
          }
          return m * n;
      }
  };
  

• class Solution:
      def maxCount(self, m: int, n: int, ops: List[List[int]]) -> int:
          for a, b in ops:
              m = min(m, a)
              n = min(n, b)
          return m * n
  
  ############
  
  from functools import reduce
  
  class Solution(object):
    def maxCount(self, m, n, ops):
      """
      :type m: int
      :type n: int
      :type ops: List[List[int]]
      :rtype: int
      """
      return reduce(operator.mul, map(min, zip(*ops + [[m, n]])))
  
  

• func maxCount(m int, n int, ops [][]int) int {
  	for _, op := range ops {
  		m = min(m, op[0])
  		n = min(n, op[1])
  	}
  	return m * n
  }
  

• function maxCount(m: number, n: number, ops: number[][]): number {
      for (const [a, b] of ops) {
          m = Math.min(m, a);
          n = Math.min(n, b);
      }
      return m * n;
  }
  
  

• /**
   * @param {number} m
   * @param {number} n
   * @param {number[][]} ops
   * @return {number}
   */
  var maxCount = function (m, n, ops) {
      for (const [a, b] of ops) {
          m = Math.min(m, a);
          n = Math.min(n, b);
      }
      return m * n;
  };
  
  

• impl Solution {
      pub fn max_count(mut m: i32, mut n: i32, ops: Vec<Vec<i32>>) -> i32 {
          for op in ops {
              m = m.min(op[0]);
              n = n.min(op[1]);
          }
          m * n
      }
  }
  
  

All Problems

All Solutions