545. Boundary of Binary Tree

Description

The boundary of a binary tree is the concatenation of the root, the left boundary, the leaves ordered from left-to-right, and the reverse order of the right boundary.

The left boundary is the set of nodes defined by the following:

The root node's left child is in the left boundary. If the root does not have a left child, then the left boundary is empty.
If a node in the left boundary and has a left child, then the left child is in the left boundary.
If a node is in the left boundary, has no left child, but has a right child, then the right child is in the left boundary.
The leftmost leaf is not in the left boundary.

The right boundary is similar to the left boundary, except it is the right side of the root's right subtree. Again, the leaf is not part of the right boundary, and the right boundary is empty if the root does not have a right child.

The leaves are nodes that do not have any children. For this problem, the root is not a leaf.

Given the root of a binary tree, return the values of its boundary.

Example 1:

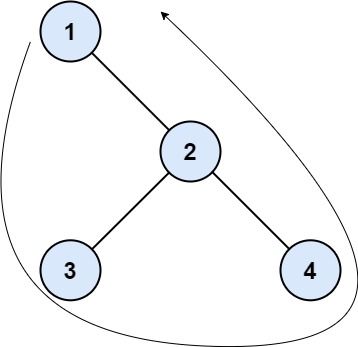
Input: root = [1,null,2,3,4]
Output: [1,3,4,2]
Explanation:
- The left boundary is empty because the root does not have a left child.
- The right boundary follows the path starting from the root's right child 2 -> 4.
  4 is a leaf, so the right boundary is [2].
- The leaves from left to right are [3,4].
Concatenating everything results in [1] + [] + [3,4] + [2] = [1,3,4,2].

Example 2:

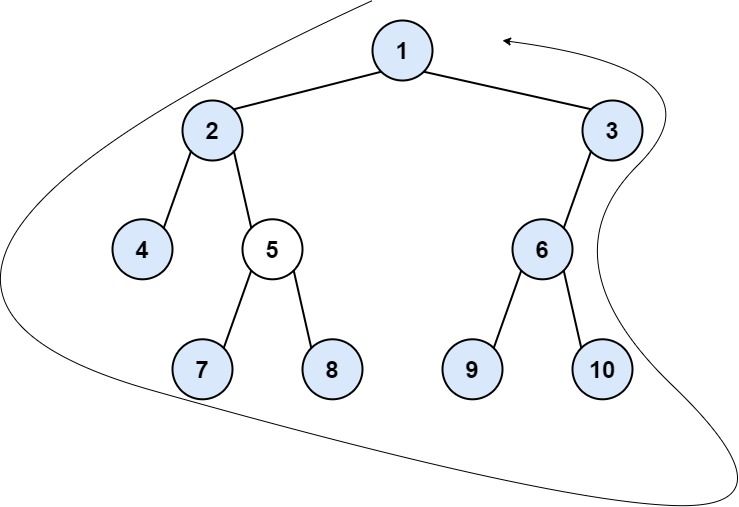
Input: root = [1,2,3,4,5,6,null,null,null,7,8,9,10]
Output: [1,2,4,7,8,9,10,6,3]
Explanation:
- The left boundary follows the path starting from the root's left child 2 -> 4.
  4 is a leaf, so the left boundary is [2].
- The right boundary follows the path starting from the root's right child 3 -> 6 -> 10.
  10 is a leaf, so the right boundary is [3,6], and in reverse order is [6,3].
- The leaves from left to right are [4,7,8,9,10].
Concatenating everything results in [1] + [2] + [4,7,8,9,10] + [6,3] = [1,2,4,7,8,9,10,6,3].

Constraints:

The number of nodes in the tree is in the range [1, 10⁴].
-1000 <= Node.val <= 1000

Solutions

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private List<Integer> res;

    public List<Integer> boundaryOfBinaryTree(TreeNode root) {
        if (root == null) {
            return Collections.emptyList();
        }
        res = new ArrayList<>();

        // root
        if (!isLeaf(root)) {
            res.add(root.val);
        }

        // left boundary
        TreeNode t = root.left;
        while (t != null) {
            if (!isLeaf(t)) {
                res.add(t.val);
            }
            t = t.left == null ? t.right : t.left;
        }

        // leaves
        addLeaves(root);

        // right boundary(reverse order)
        Deque<Integer> s = new ArrayDeque<>();
        t = root.right;
        while (t != null) {
            if (!isLeaf(t)) {
                s.offer(t.val);
            }
            t = t.right == null ? t.left : t.right;
        }
        while (!s.isEmpty()) {
            res.add(s.pollLast());
        }

        // output
        return res;
    }

    private void addLeaves(TreeNode root) {
        if (isLeaf(root)) {
            res.add(root.val);
            return;
        }
        if (root.left != null) {
            addLeaves(root.left);
        }
        if (root.right != null) {
            addLeaves(root.right);
        }
    }

    private boolean isLeaf(TreeNode node) {
        return node != null && node.left == null && node.right == null;
    }
}

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def boundaryOfBinaryTree(self, root: TreeNode) -> List[int]:
        self.res = []
        if not root:
            return self.res
        # root
        if not self.is_leaf(root):
            self.res.append(root.val)

        # left boundary
        t = root.left
        while t:
            if not self.is_leaf(t):
                self.res.append(t.val)
            t = t.left if t.left else t.right

        # leaves
        self.add_leaves(root)

        # right boundary(reverse order)
        s = []
        t = root.right
        while t:
            if not self.is_leaf(t):
                s.append(t.val)
            t = t.right if t.right else t.left
        while s:
            self.res.append(s.pop())

        # output
        return self.res

    def add_leaves(self, root):
        if self.is_leaf(root):
            self.res.append(root.val)
            return
        if root.left:
            self.add_leaves(root.left)
        if root.right:
            self.add_leaves(root.right)

    def is_leaf(self, node) -> bool:
        return node and node.left is None and node.right is None

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var boundaryOfBinaryTree = function (root) {
    let leftBoundary = function (root, res) {
        while (root) {
            let curVal = root.val;
            if (root.left) {
                root = root.left;
            } else if (root.right) {
                root = root.right;
            } else {
                break;
            }
            res.push(curVal);
        }
    };
    let rightBoundary = function (root, res) {
        let stk = [];
        while (root) {
            let curVal = root.val;
            if (root.right) {
                root = root.right;
            } else if (root.left) {
                root = root.left;
            } else {
                break;
            }
            stk.push(curVal);
        }
        let len = stk.length;
        for (let i = 0; i < len; i++) {
            res.push(stk.pop());
        }
    };
    let levelBoundary = function (root, res) {
        if (root) {
            levelBoundary(root.left, res);
            if (!root.left && !root.right) {
                res.push(root.val);
            }
            levelBoundary(root.right, res);
        }
    };
    let res = [];
    if (root) {
        res.push(root.val);
        leftBoundary(root.left, res);
        if (root.left || root.right) {
            levelBoundary(root, res);
        }
        rightBoundary(root.right, res);
    }
    return res;
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> boundaryOfBinaryTree(TreeNode* root) {
        auto dfs = [&](auto&& dfs, vector<int>& nums, TreeNode* root, int i) -> void {
            if (!root) {
                return;
            }
            if (i == 0) {
                if (root->left != root->right) {
                    nums.push_back(root->val);
                    if (root->left) {
                        dfs(dfs, nums, root->left, i);
                    } else {
                        dfs(dfs, nums, root->right, i);
                    }
                }
            } else if (i == 1) {
                if (root->left == root->right) {
                    nums.push_back(root->val);
                } else {
                    dfs(dfs, nums, root->left, i);
                    dfs(dfs, nums, root->right, i);
                }
            } else {
                if (root->left != root->right) {
                    nums.push_back(root->val);
                    if (root->right) {
                        dfs(dfs, nums, root->right, i);
                    } else {
                        dfs(dfs, nums, root->left, i);
                    }
                }
            }
        };
        vector<int> ans = {root->val};
        if (root->left == root->right) {
            return ans;
        }
        vector<int> left, right, leaves;
        dfs(dfs, left, root->left, 0);
        dfs(dfs, leaves, root, 1);
        dfs(dfs, right, root->right, 2);
        ans.insert(ans.end(), left.begin(), left.end());
        ans.insert(ans.end(), leaves.begin(), leaves.end());
        ans.insert(ans.end(), right.rbegin(), right.rend());
        return ans;
    }
};

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func boundaryOfBinaryTree(root *TreeNode) []int {
	ans := []int{root.Val}
	if root.Left == root.Right {
		return ans
	}

	left, leaves, right := []int{}, []int{}, []int{}

	var dfs func(nums *[]int, root *TreeNode, i int)
	dfs = func(nums *[]int, root *TreeNode, i int) {
		if root == nil {
			return
		}
		if i == 0 {
			if root.Left != root.Right {
				*nums = append(*nums, root.Val)
				if root.Left != nil {
					dfs(nums, root.Left, i)
				} else {
					dfs(nums, root.Right, i)
				}
			}
		} else if i == 1 {
			if root.Left == root.Right {
				*nums = append(*nums, root.Val)
			} else {
				dfs(nums, root.Left, i)
				dfs(nums, root.Right, i)
			}
		} else {
			if root.Left != root.Right {
				*nums = append(*nums, root.Val)
				if root.Right != nil {
					dfs(nums, root.Right, i)
				} else {
					dfs(nums, root.Left, i)
				}
			}
		}
	}

	dfs(&left, root.Left, 0)
	dfs(&leaves, root, 1)
	dfs(&right, root.Right, 2)

	ans = append(ans, left...)
	ans = append(ans, leaves...)
	for i := len(right) - 1; i >= 0; i-- {
		ans = append(ans, right[i])
	}

	return ans
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function boundaryOfBinaryTree(root: TreeNode | null): number[] {
    const ans: number[] = [root.val];
    if (root.left === root.right) {
        return ans;
    }

    const left: number[] = [];
    const leaves: number[] = [];
    const right: number[] = [];

    const dfs = function (nums: number[], root: TreeNode | null, i: number) {
        if (!root) {
            return;
        }
        if (i === 0) {
            if (root.left !== root.right) {
                nums.push(root.val);
                if (root.left) {
                    dfs(nums, root.left, i);
                } else {
                    dfs(nums, root.right, i);
                }
            }
        } else if (i === 1) {
            if (root.left === root.right) {
                nums.push(root.val);
            } else {
                dfs(nums, root.left, i);
                dfs(nums, root.right, i);
            }
        } else {
            if (root.left !== root.right) {
                nums.push(root.val);
                if (root.right) {
                    dfs(nums, root.right, i);
                } else {
                    dfs(nums, root.left, i);
                }
            }
        }
    };

    dfs(left, root.left, 0);
    dfs(leaves, root, 1);
    dfs(right, root.right, 2);

    return ans.concat(left).concat(leaves).concat(right.reverse());
}

545 - Boundary of Binary Tree

545. Boundary of Binary Tree

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

545. Boundary of Binary Tree

Description

Solutions

All Problems

All Solutions