542. 01 Matrix

Description

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Example 1:

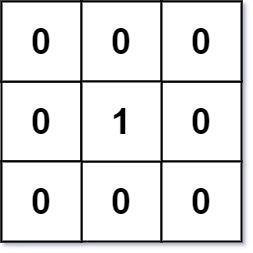
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

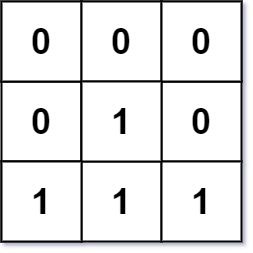
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 10⁴
1 <= m * n <= 10⁴
mat[i][j] is either 0 or 1.
There is at least one 0 in mat.

Solutions

Method One: Multi-source BFS

Initialize the result matrix ans, where the distance of all zeros is 0, and thus the distance of all ones is -1.

Initialize a queue q to store the positions to be checked by BFS, and enqueue all positions of zeros.

Continually dequeue elements p(i, j) from queue q, inspecting the four neighboring points.

For each neighbor (x, y), if ans[x][y] = -1, then update ans[x][y] = ans[i][j] + 1.

Also, enqueue the position (x, y).

class Solution {
    public int[][] updateMatrix(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[][] ans = new int[m][n];
        for (int[] row : ans) {
            Arrays.fill(row, -1);
        }
        Deque<int[]> q = new ArrayDeque<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 0) {
                    q.offer(new int[] {i, j});
                    ans[i][j] = 0;
                }
            }
        }
        int[] dirs = {-1, 0, 1, 0, -1};
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int i = p[0], j = p[1];
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1) {
                    ans[x][y] = ans[i][j] + 1;
                    q.offer(new int[] {x, y});
                }
            }
        }
        return ans;
    }
}

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> ans(m, vector<int>(n, -1));
        queue<pair<int, int>> q;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 0) {
                    ans[i][j] = 0;
                    q.emplace(i, j);
                }
            }
        }
        vector<int> dirs = {-1, 0, 1, 0, -1};
        while (!q.empty()) {
            auto p = q.front();
            q.pop();
            for (int i = 0; i < 4; ++i) {
                int x = p.first + dirs[i];
                int y = p.second + dirs[i + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1) {
                    ans[x][y] = ans[p.first][p.second] + 1;
                    q.emplace(x, y);
                }
            }
        }
        return ans;
    }
};

class Solution:
    def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
        m, n = len(mat), len(mat[0])
        ans = [[-1] * n for _ in range(m)]
        q = deque()
        for i, row in enumerate(mat):
            for j, x in enumerate(row):
                if x == 0:
                    ans[i][j] = 0
                    q.append((i, j))
        dirs = (-1, 0, 1, 0, -1)
        while q:
            i, j = q.popleft()
            for a, b in pairwise(dirs):
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and ans[x][y] == -1:
                    ans[x][y] = ans[i][j] + 1
                    q.append((x, y))
        return ans

func updateMatrix(mat [][]int) [][]int {
	m, n := len(mat), len(mat[0])
	ans := make([][]int, m)
	for i := range ans {
		ans[i] = make([]int, n)
		for j := range ans[i] {
			ans[i][j] = -1
		}
	}
	type pair struct{ x, y int }
	var q []pair
	for i, row := range mat {
		for j, v := range row {
			if v == 0 {
				ans[i][j] = 0
				q = append(q, pair{i, j})
			}
		}
	}
	dirs := []int{-1, 0, 1, 0, -1}
	for len(q) > 0 {
		p := q[0]
		q = q[1:]
		for i := 0; i < 4; i++ {
			x, y := p.x+dirs[i], p.y+dirs[i+1]
			if x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1 {
				ans[x][y] = ans[p.x][p.y] + 1
				q = append(q, pair{x, y})
			}
		}
	}
	return ans
}

function updateMatrix(mat: number[][]): number[][] {
    const [m, n] = [mat.length, mat[0].length];
    const ans: number[][] = Array.from({ length: m }, () => Array.from({ length: n }, () => -1));
    const q: [number, number][] = [];
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (mat[i][j] === 0) {
                q.push([i, j]);
                ans[i][j] = 0;
            }
        }
    }
    const dirs: number[] = [-1, 0, 1, 0, -1];
    while (q.length) {
        const [i, j] = q.shift()!;
        for (let k = 0; k < 4; ++k) {
            const [x, y] = [i + dirs[k], j + dirs[k + 1]];
            if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] === -1) {
                ans[x][y] = ans[i][j] + 1;
                q.push([x, y]);
            }
        }
    }
    return ans;
}

use std::collections::VecDeque;

impl Solution {
    #[allow(dead_code)]
    pub fn update_matrix(mat: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let n: usize = mat.len();
        let m: usize = mat[0].len();
        let mut ret_vec: Vec<Vec<i32>> = vec![vec![-1; m]; n];
        // The inner tuple is of <X, Y, Current Count>
        let mut the_q: VecDeque<(usize, usize)> = VecDeque::new();
        let traverse_vec: Vec<(i32, i32)> = vec![(-1, 0), (1, 0), (0, 1), (0, -1)];

        // Initialize the queue
        for i in 0..n {
            for j in 0..m {
                if mat[i][j] == 0 {
                    // For the zero cell, enqueue at first
                    the_q.push_back((i, j));
                    // Set to 0 in return vector
                    ret_vec[i][j] = 0;
                }
            }
        }

        while !the_q.is_empty() {
            let (x, y) = the_q.front().unwrap().clone();
            the_q.pop_front();
            for pair in &traverse_vec {
                let cur_x = pair.0 + (x as i32);
                let cur_y = pair.1 + (y as i32);
                if
                    Solution::check_bounds(cur_x, cur_y, n as i32, m as i32) &&
                    ret_vec[cur_x as usize][cur_y as usize] == -1
                {
                    // The current cell has not be updated yet, and is also in bound
                    ret_vec[cur_x as usize][cur_y as usize] = ret_vec[x][y] + 1;
                    the_q.push_back((cur_x as usize, cur_y as usize));
                }
            }
        }

        ret_vec
    }

    #[allow(dead_code)]
    pub fn check_bounds(i: i32, j: i32, n: i32, m: i32) -> bool {
        i >= 0 && i < n && j >= 0 && j < m
    }
}

542 - 01 Matrix

542. 01 Matrix

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

542. 01 Matrix

Description

Solutions

All Problems

All Solutions