Welcome to Subscribe On Youtube

497. Random Point in Non-overlapping Rectangles

Description

You are given an array of non-overlapping axis-aligned rectangles rects where rects[i] = [ai, bi, xi, yi] indicates that (ai, bi) is the bottom-left corner point of the ith rectangle and (xi, yi) is the top-right corner point of the ith rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.

Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.

Note that an integer point is a point that has integer coordinates.

Implement the Solution class:

• Solution(int[][] rects) Initializes the object with the given rectangles rects.
• int[] pick() Returns a random integer point [u, v] inside the space covered by one of the given rectangles.

 

Example 1:

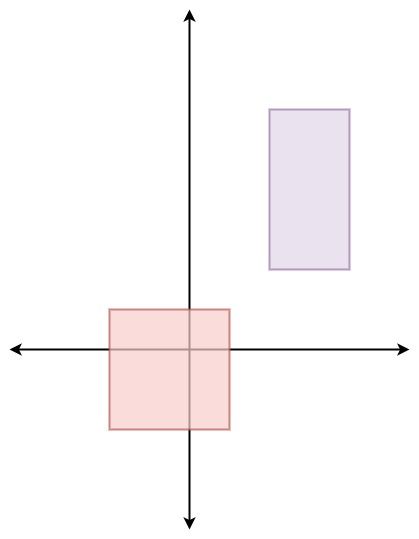
Input
["Solution", "pick", "pick", "pick", "pick", "pick"]
[[[[-2, -2, 1, 1], [2, 2, 4, 6]]], [], [], [], [], []]
Output
[null, [1, -2], [1, -1], [-1, -2], [-2, -2], [0, 0]]

Explanation
Solution solution = new Solution([[-2, -2, 1, 1], [2, 2, 4, 6]]);
solution.pick(); // return [1, -2]
solution.pick(); // return [1, -1]
solution.pick(); // return [-1, -2]
solution.pick(); // return [-2, -2]
solution.pick(); // return [0, 0]

 

Constraints:

• 1 <= rects.length <= 100
• rects[i].length == 4
• -109 <= ai < xi <= 109
• -109 <= bi < yi <= 109
• xi - ai <= 2000
• yi - bi <= 2000
• All the rectangles do not overlap.
• At most 104 calls will be made to pick.

Solutions

• Java
• C++
• Python
• Go

• class Solution {
      private int[] s;
      private int[][] rects;
      private Random random = new Random();
  
      public Solution(int[][] rects) {
          int n = rects.length;
          s = new int[n + 1];
          for (int i = 0; i < n; ++i) {
              s[i + 1] = s[i] + (rects[i][2] - rects[i][0] + 1) * (rects[i][3] - rects[i][1] + 1);
          }
          this.rects = rects;
      }
  
      public int[] pick() {
          int n = rects.length;
          int v = 1 + random.nextInt(s[n]);
          int left = 0, right = n;
          while (left < right) {
              int mid = (left + right) >> 1;
              if (s[mid] >= v) {
                  right = mid;
              } else {
                  left = mid + 1;
              }
          }
          int[] rect = rects[left - 1];
          return new int[] {rect[0] + random.nextInt(rect[2] - rect[0] + 1),
              rect[1] + random.nextInt(rect[3] - rect[1] + 1)};
      }
  }
  
  /**
   * Your Solution object will be instantiated and called as such:
   * Solution obj = new Solution(rects);
   * int[] param_1 = obj.pick();
   */
  

• class Solution {
  public:
      vector<int> s;
      vector<vector<int>> rects;
  
      Solution(vector<vector<int>>& rects) {
          int n = rects.size();
          s.resize(n + 1);
          for (int i = 0; i < n; ++i) s[i + 1] = s[i] + (rects[i][2] - rects[i][0] + 1) * (rects[i][3] - rects[i][1] + 1);
          this->rects = rects;
          srand(time(nullptr));
      }
  
      vector<int> pick() {
          int n = rects.size();
          int v = 1 + rand() % s[n];
          int idx = lower_bound(s.begin(), s.end(), v) - s.begin();
          auto& rect = rects[idx - 1];
          int x = rect[0] + rand() % (rect[2] - rect[0] + 1);
          int y = rect[1] + rand() % (rect[3] - rect[1] + 1);
          return {x, y};
      }
  };
  
  /**
   * Your Solution object will be instantiated and called as such:
   * Solution* obj = new Solution(rects);
   * vector<int> param_1 = obj->pick();
   */
  

• class Solution:
      def __init__(self, rects: List[List[int]]):
          self.rects = rects
          self.s = [0] * len(rects)
          for i, (x1, y1, x2, y2) in enumerate(rects):
              self.s[i] = self.s[i - 1] + (x2 - x1 + 1) * (y2 - y1 + 1)
  
      def pick(self) -> List[int]:
          v = random.randint(1, self.s[-1])
          idx = bisect_left(self.s, v)
          x1, y1, x2, y2 = self.rects[idx]
          return [random.randint(x1, x2), random.randint(y1, y2)]
  
  
  # Your Solution object will be instantiated and called as such:
  # obj = Solution(rects)
  # param_1 = obj.pick()
  
  

• type Solution struct {
  	s     []int
  	rects [][]int
  }
  
  func Constructor(rects [][]int) Solution {
  	n := len(rects)
  	s := make([]int, n+1)
  	for i, v := range rects {
  		s[i+1] = s[i] + (v[2]-v[0]+1)*(v[3]-v[1]+1)
  	}
  	return Solution{s, rects}
  }
  
  func (this *Solution) Pick() []int {
  	n := len(this.rects)
  	v := 1 + rand.Intn(this.s[len(this.s)-1])
  	left, right := 0, n
  	for left < right {
  		mid := (left + right) >> 1
  		if this.s[mid] >= v {
  			right = mid
  		} else {
  			left = mid + 1
  		}
  	}
  	rect := this.rects[left-1]
  	x, y := rect[0]+rand.Intn(rect[2]-rect[0]+1), rect[1]+rand.Intn(rect[3]-rect[1]+1)
  	return []int{x, y}
  }
  

All Problems

All Solutions