Welcome to Subscribe On Youtube

469. Convex Polygon

Description

You are given an array of points on the X-Y plane points where points[i] = [xi, yi]. The points form a polygon when joined sequentially.

Return true if this polygon is convex and false otherwise.

You may assume the polygon formed by given points is always a simple polygon. In other words, we ensure that exactly two edges intersect at each vertex and that edges otherwise don't intersect each other.

 

Example 1:

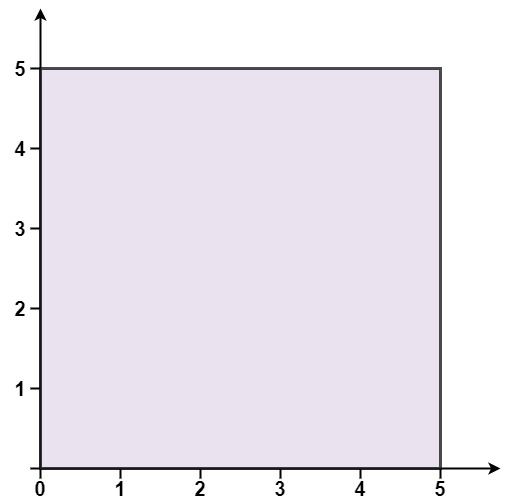
Input: points = [[0,0],[0,5],[5,5],[5,0]]
Output: true

Example 2:

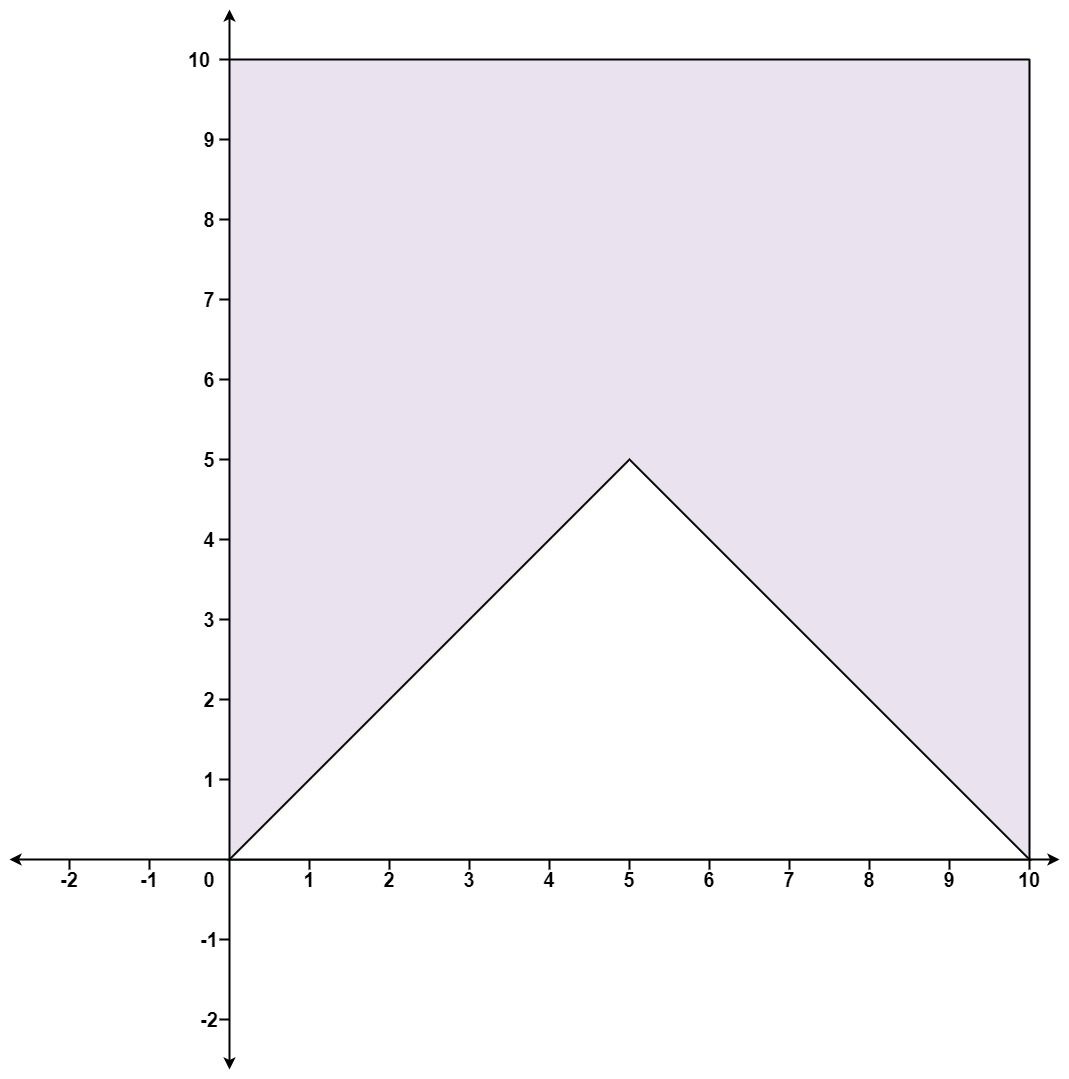
Input: points = [[0,0],[0,10],[10,10],[10,0],[5,5]]
Output: false

 

Constraints:

• 3 <= points.length <= 104
• points[i].length == 2
• -104 <= xi, yi <= 104
• All the given points are unique.

Solutions

• Java
• C++
• Python
• Go

• class Solution {
      public boolean isConvex(List<List<Integer>> points) {
          int n = points.size();
          long pre = 0, cur = 0;
          for (int i = 0; i < n; ++i) {
              var p1 = points.get(i);
              var p2 = points.get((i + 1) % n);
              var p3 = points.get((i + 2) % n);
              int x1 = p2.get(0) - p1.get(0);
              int y1 = p2.get(1) - p1.get(1);
              int x2 = p3.get(0) - p1.get(0);
              int y2 = p3.get(1) - p1.get(1);
              cur = x1 * y2 - x2 * y1;
              if (cur != 0) {
                  if (cur * pre < 0) {
                      return false;
                  }
                  pre = cur;
              }
          }
          return true;
      }
  }
  

• class Solution {
  public:
      bool isConvex(vector<vector<int>>& points) {
          int n = points.size();
          long long pre = 0, cur = 0;
          for (int i = 0; i < n; ++i) {
              int x1 = points[(i + 1) % n][0] - points[i][0];
              int y1 = points[(i + 1) % n][1] - points[i][1];
              int x2 = points[(i + 2) % n][0] - points[i][0];
              int y2 = points[(i + 2) % n][1] - points[i][1];
              cur = 1L * x1 * y2 - x2 * y1;
              if (cur != 0) {
                  if (cur * pre < 0) {
                      return false;
                  }
                  pre = cur;
              }
          }
          return true;
      }
  };
  

• class Solution:
      def isConvex(self, points: List[List[int]]) -> bool:
          n = len(points)
          pre = cur = 0
          for i in range(n):
              x1 = points[(i + 1) % n][0] - points[i][0]
              y1 = points[(i + 1) % n][1] - points[i][1]
              x2 = points[(i + 2) % n][0] - points[i][0]
              y2 = points[(i + 2) % n][1] - points[i][1]
              cur = x1 * y2 - x2 * y1
              if cur != 0:
                  if cur * pre < 0:
                      return False
                  pre = cur
          return True
  
  

• func isConvex(points [][]int) bool {
  	n := len(points)
  	pre, cur := 0, 0
  	for i := range points {
  		x1 := points[(i+1)%n][0] - points[i][0]
  		y1 := points[(i+1)%n][1] - points[i][1]
  		x2 := points[(i+2)%n][0] - points[i][0]
  		y2 := points[(i+2)%n][1] - points[i][1]
  		cur = x1*y2 - x2*y1
  		if cur != 0 {
  			if cur*pre < 0 {
  				return false
  			}
  			pre = cur
  		}
  	}
  	return true
  }
  

All Problems

All Solutions