Welcome to Subscribe On Youtube
391. Perfect Rectangle
Description
Given an array rectangles where rectangles[i] = [xi, yi, ai, bi] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (xi, yi) and the top-right point of it is (ai, bi).
Return true if all the rectangles together form an exact cover of a rectangular region.
Example 1:
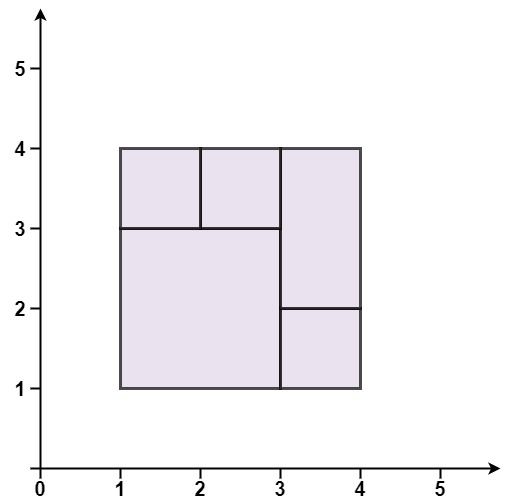
Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]] Output: true Explanation: All 5 rectangles together form an exact cover of a rectangular region.
Example 2:
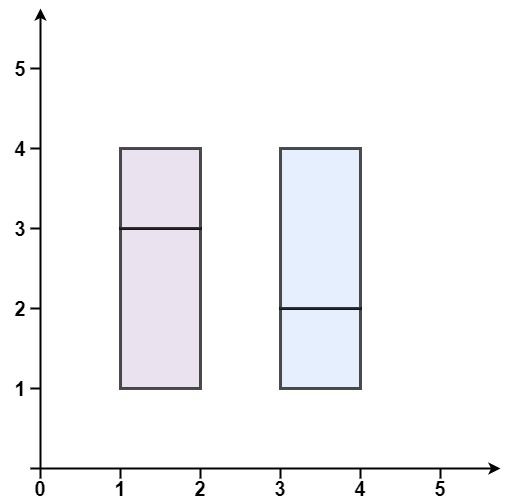
Input: rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]] Output: false Explanation: Because there is a gap between the two rectangular regions.
Example 3:
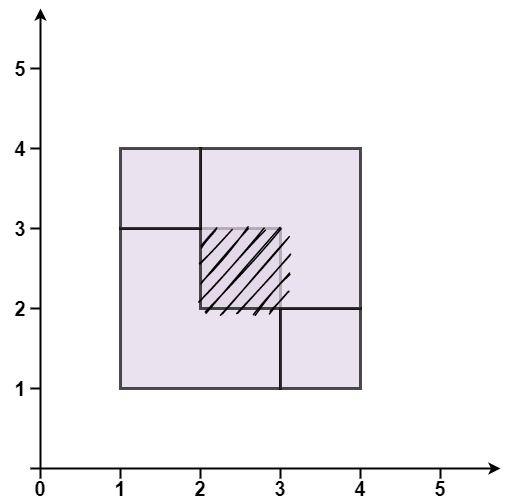
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]] Output: false Explanation: Because two of the rectangles overlap with each other.
Constraints:
1 <= rectangles.length <= 2 * 104rectangles[i].length == 4-105 <= xi, yi, ai, bi <= 105
Solutions
-
class Solution { public boolean isRectangleCover(int[][] rectangles) { long area = 0; int minX = rectangles[0][0], minY = rectangles[0][1]; int maxX = rectangles[0][2], maxY = rectangles[0][3]; Map<Pair, Integer> cnt = new HashMap<>(); for (int[] r : rectangles) { area += (r[2] - r[0]) * (r[3] - r[1]); minX = Math.min(minX, r[0]); minY = Math.min(minY, r[1]); maxX = Math.max(maxX, r[2]); maxY = Math.max(maxY, r[3]); cnt.merge(new Pair(r[0], r[1]), 1, Integer::sum); cnt.merge(new Pair(r[0], r[3]), 1, Integer::sum); cnt.merge(new Pair(r[2], r[3]), 1, Integer::sum); cnt.merge(new Pair(r[2], r[1]), 1, Integer::sum); } if (area != (long) (maxX - minX) * (maxY - minY) || cnt.getOrDefault(new Pair(minX, minY), 0) != 1 || cnt.getOrDefault(new Pair(minX, maxY), 0) != 1 || cnt.getOrDefault(new Pair(maxX, maxY), 0) != 1 || cnt.getOrDefault(new Pair(maxX, minY), 0) != 1) { return false; } cnt.remove(new Pair(minX, minY)); cnt.remove(new Pair(minX, maxY)); cnt.remove(new Pair(maxX, maxY)); cnt.remove(new Pair(maxX, minY)); return cnt.values().stream().allMatch(c -> c == 2 || c == 4); } private static class Pair { final int first; final int second; Pair(int first, int second) { this.first = first; this.second = second; } @Override public boolean equals(Object o) { if (this == o) { return true; } if (o == null || getClass() != o.getClass()) { return false; } Pair pair = (Pair) o; return first == pair.first && second == pair.second; } @Override public int hashCode() { return Objects.hash(first, second); } } } -
#include <bits/stdc++.h> using namespace std; class Solution { public: bool isRectangleCover(vector<vector<int>>& rectangles) { long long area = 0; int minX = rectangles[0][0], minY = rectangles[0][1]; int maxX = rectangles[0][2], maxY = rectangles[0][3]; using pii = pair<int, int>; map<pii, int> cnt; for (auto& r : rectangles) { area += (r[2] - r[0]) * (r[3] - r[1]); minX = min(minX, r[0]); minY = min(minY, r[1]); maxX = max(maxX, r[2]); maxY = max(maxY, r[3]); ++cnt[{r[0], r[1]}]; ++cnt[{r[0], r[3]}]; ++cnt[{r[2], r[3]}]; ++cnt[{r[2], r[1]}]; } if (area != (long long) (maxX - minX) * (maxY - minY) || cnt[{minX, minY}] != 1 || cnt[{minX, maxY}] != 1 || cnt[{maxX, maxY}] != 1 || cnt[{maxX, minY}] != 1) { return false; } cnt.erase({minX, minY}); cnt.erase({minX, maxY}); cnt.erase({maxX, maxY}); cnt.erase({maxX, minY}); return all_of(cnt.begin(), cnt.end(), [](pair<pii, int> e) { return e.second == 2 || e.second == 4; }); } }; -
class Solution: def isRectangleCover(self, rectangles: List[List[int]]) -> bool: area = 0 minX, minY = rectangles[0][0], rectangles[0][1] maxX, maxY = rectangles[0][2], rectangles[0][3] cnt = defaultdict(int) for r in rectangles: area += (r[2] - r[0]) * (r[3] - r[1]) minX = min(minX, r[0]) minY = min(minY, r[1]) maxX = max(maxX, r[2]) maxY = max(maxY, r[3]) cnt[(r[0], r[1])] += 1 cnt[(r[0], r[3])] += 1 cnt[(r[2], r[3])] += 1 cnt[(r[2], r[1])] += 1 if ( area != (maxX - minX) * (maxY - minY) or cnt[(minX, minY)] != 1 or cnt[(minX, maxY)] != 1 or cnt[(maxX, maxY)] != 1 or cnt[(maxX, minY)] != 1 ): return False del cnt[(minX, minY)], cnt[(minX, maxY)], cnt[(maxX, maxY)], cnt[(maxX, minY)] return all(c == 2 or c == 4 for c in cnt.values()) -
type pair struct { first int second int } func isRectangleCover(rectangles [][]int) bool { area := 0 minX, minY := rectangles[0][0], rectangles[0][1] maxX, maxY := rectangles[0][2], rectangles[0][3] cnt := make(map[pair]int) for _, r := range rectangles { area += (r[2] - r[0]) * (r[3] - r[1]) minX = min(minX, r[0]) minY = min(minY, r[1]) maxX = max(maxX, r[2]) maxY = max(maxY, r[3]) cnt[pair{r[0], r[1]}]++ cnt[pair{r[0], r[3]}]++ cnt[pair{r[2], r[3]}]++ cnt[pair{r[2], r[1]}]++ } if area != (maxX-minX)*(maxY-minY) || cnt[pair{minX, minY}] != 1 || cnt[pair{minX, maxY}] != 1 || cnt[pair{maxX, maxY}] != 1 || cnt[pair{maxX, minY}] != 1 { return false } delete(cnt, pair{minX, minY}) delete(cnt, pair{minX, maxY}) delete(cnt, pair{maxX, maxY}) delete(cnt, pair{maxX, minY}) for _, c := range cnt { if c != 2 && c != 4 { return false } } return true }