Welcome to Subscribe On Youtube

356. Line Reflection

Description

Given n points on a 2D plane, find if there is such a line parallel to the y-axis that reflects the given points symmetrically.

In other words, answer whether or not if there exists a line that after reflecting all points over the given line, the original points' set is the same as the reflected ones.

Note that there can be repeated points.

 

Example 1:

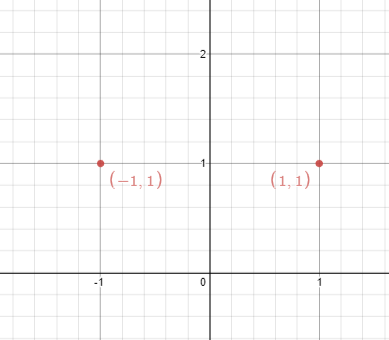
Input: points = [[1,1],[-1,1]]
Output: true
Explanation: We can choose the line x = 0.

Example 2:

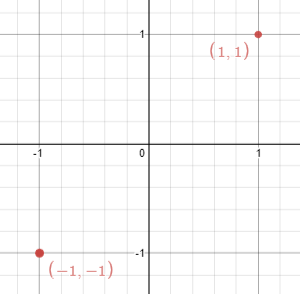
Input: points = [[1,1],[-1,-1]]
Output: false
Explanation: We can't choose a line.

 

Constraints:

• n == points.length
• 1 <= n <= 104
• -108 <= points[i][j] <= 108

 

Follow up: Could you do better than O(n2)?

Solutions

• Java
• C++
• Python
• Go

• class Solution {
      public boolean isReflected(int[][] points) {
          final int inf = 1 << 30;
          int minX = inf, maxX = -inf;
          Set<List<Integer>> pointSet = new HashSet<>();
          for (int[] p : points) {
              minX = Math.min(minX, p[0]);
              maxX = Math.max(maxX, p[0]);
              pointSet.add(List.of(p[0], p[1]));
          }
          int s = minX + maxX;
          for (int[] p : points) {
              if (!pointSet.contains(List.of(s - p[0], p[1]))) {
                  return false;
              }
          }
          return true;
      }
  }
  

• class Solution {
  public:
      bool isReflected(vector<vector<int>>& points) {
          const int inf = 1 << 30;
          int minX = inf, maxX = -inf;
          set<pair<int, int>> pointSet;
          for (auto& p : points) {
              minX = min(minX, p[0]);
              maxX = max(maxX, p[0]);
              pointSet.insert({p[0], p[1]});
          }
          int s = minX + maxX;
          for (auto& p : points) {
              if (!pointSet.count({s - p[0], p[1]})) {
                  return false;
              }
          }
          return true;
      }
  };
  

• class Solution:
      def isReflected(self, points: List[List[int]]) -> bool:
          min_x, max_x = inf, -inf
          point_set = set()
          for x, y in points:
              min_x = min(min_x, x)
              max_x = max(max_x, x)
              point_set.add((x, y))
          s = min_x + max_x
          return all((s - x, y) in point_set for x, y in points)
  
  

• func isReflected(points [][]int) bool {
  	const inf = 1 << 30
  	minX, maxX := inf, -inf
  	pointSet := map[[2]int]bool{}
  	for _, p := range points {
  		minX = min(minX, p[0])
  		maxX = max(maxX, p[0])
  		pointSet[[2]int{p[0], p[1]}] = true
  	}
  	s := minX + maxX
  	for _, p := range points {
  		if !pointSet[[2]int{s - p[0], p[1]}] {
  			return false
  		}
  	}
  	return true
  }
  

All Problems

All Solutions