Welcome to Subscribe On Youtube

351. Android Unlock Patterns

Description

Android devices have a special lock screen with a 3 x 3 grid of dots. Users can set an "unlock pattern" by connecting the dots in a specific sequence, forming a series of joined line segments where each segment's endpoints are two consecutive dots in the sequence. A sequence of k dots is a valid unlock pattern if both of the following are true:

• All the dots in the sequence are distinct.
• If the line segment connecting two consecutive dots in the sequence passes through the center of any other dot, the other dot must have previously appeared in the sequence. No jumps through the center non-selected dots are allowed.
  • For example, connecting dots 2 and 9 without dots 5 or 6 appearing beforehand is valid because the line from dot 2 to dot 9 does not pass through the center of either dot 5 or 6.
  • However, connecting dots 1 and 3 without dot 2 appearing beforehand is invalid because the line from dot 1 to dot 3 passes through the center of dot 2.

Here are some example valid and invalid unlock patterns:

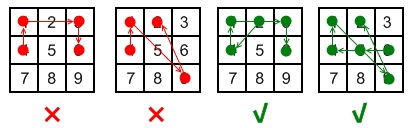
• The 1st pattern [4,1,3,6] is invalid because the line connecting dots 1 and 3 pass through dot 2, but dot 2 did not previously appear in the sequence.
• The 2nd pattern [4,1,9,2] is invalid because the line connecting dots 1 and 9 pass through dot 5, but dot 5 did not previously appear in the sequence.
• The 3rd pattern [2,4,1,3,6] is valid because it follows the conditions. The line connecting dots 1 and 3 meets the condition because dot 2 previously appeared in the sequence.
• The 4th pattern [6,5,4,1,9,2] is valid because it follows the conditions. The line connecting dots 1 and 9 meets the condition because dot 5 previously appeared in the sequence.

Given two integers m and n, return the number of unique and valid unlock patterns of the Android grid lock screen that consist of at least m keys and at most n keys.

Two unlock patterns are considered unique if there is a dot in one sequence that is not in the other, or the order of the dots is different.

 

Example 1:

Input: m = 1, n = 1
Output: 9

Example 2:

Input: m = 1, n = 2
Output: 65

 

Constraints:

• 1 <= m, n <= 9

Solutions

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      private int m;
      private int n;
      private int[][] cross = new int[10][10];
      private boolean[] vis = new boolean[10];
  
      public int numberOfPatterns(int m, int n) {
          this.m = m;
          this.n = n;
          cross[1][3] = cross[3][1] = 2;
          cross[1][7] = cross[7][1] = 4;
          cross[1][9] = cross[9][1] = 5;
          cross[2][8] = cross[8][2] = 5;
          cross[3][7] = cross[7][3] = 5;
          cross[3][9] = cross[9][3] = 6;
          cross[4][6] = cross[6][4] = 5;
          cross[7][9] = cross[9][7] = 8;
          return dfs(1, 1) * 4 + dfs(2, 1) * 4 + dfs(5, 1);
      }
  
      private int dfs(int i, int cnt) {
          if (cnt > n) {
              return 0;
          }
          vis[i] = true;
          int ans = cnt >= m ? 1 : 0;
          for (int j = 1; j < 10; ++j) {
              int x = cross[i][j];
              if (!vis[j] && (x == 0 || vis[x])) {
                  ans += dfs(j, cnt + 1);
              }
          }
          vis[i] = false;
          return ans;
      }
  }
  

• class Solution {
  public:
      int numberOfPatterns(int m, int n) {
          int cross[10][10];
          memset(cross, 0, sizeof(cross));
          bool vis[10];
          memset(vis, false, sizeof(vis));
          cross[1][3] = cross[3][1] = 2;
          cross[1][7] = cross[7][1] = 4;
          cross[1][9] = cross[9][1] = 5;
          cross[2][8] = cross[8][2] = 5;
          cross[3][7] = cross[7][3] = 5;
          cross[3][9] = cross[9][3] = 6;
          cross[4][6] = cross[6][4] = 5;
          cross[7][9] = cross[9][7] = 8;
  
          function<int(int, int)> dfs = [&](int i, int cnt) {
              if (cnt > n) {
                  return 0;
              }
              vis[i] = true;
              int ans = cnt >= m ? 1 : 0;
              for (int j = 1; j < 10; ++j) {
                  int x = cross[i][j];
                  if (!vis[j] && (x == 0 || vis[x])) {
                      ans += dfs(j, cnt + 1);
                  }
              }
              vis[i] = false;
              return ans;
          };
  
          return dfs(1, 1) * 4 + dfs(2, 1) * 4 + dfs(5, 1);
      }
  };
  

• class Solution:
      def numberOfPatterns(self, m: int, n: int) -> int:
          def dfs(i: int, cnt: int = 1) -> int:
              if cnt > n:
                  return 0
              vis[i] = True
              ans = int(cnt >= m)
              for j in range(1, 10):
                  x = cross[i][j]
                  if not vis[j] and (x == 0 or vis[x]):
                      ans += dfs(j, cnt + 1)
              vis[i] = False
              return ans
  
          cross = [[0] * 10 for _ in range(10)]
          cross[1][3] = cross[3][1] = 2
          cross[1][7] = cross[7][1] = 4
          cross[1][9] = cross[9][1] = 5
          cross[2][8] = cross[8][2] = 5
          cross[3][7] = cross[7][3] = 5
          cross[3][9] = cross[9][3] = 6
          cross[4][6] = cross[6][4] = 5
          cross[7][9] = cross[9][7] = 8
          vis = [False] * 10
          return dfs(1) * 4 + dfs(2) * 4 + dfs(5)
  
  

• func numberOfPatterns(m int, n int) int {
  	cross := [10][10]int{}
  	vis := [10]bool{}
  	cross[1][3] = 2
  	cross[1][7] = 4
  	cross[1][9] = 5
  	cross[2][8] = 5
  	cross[3][7] = 5
  	cross[3][9] = 6
  	cross[4][6] = 5
  	cross[7][9] = 8
  	cross[3][1] = 2
  	cross[7][1] = 4
  	cross[9][1] = 5
  	cross[8][2] = 5
  	cross[7][3] = 5
  	cross[9][3] = 6
  	cross[6][4] = 5
  	cross[9][7] = 8
  	var dfs func(int, int) int
  	dfs = func(i, cnt int) int {
  		if cnt > n {
  			return 0
  		}
  		vis[i] = true
  		ans := 0
  		if cnt >= m {
  			ans++
  		}
  		for j := 1; j < 10; j++ {
  			x := cross[i][j]
  			if !vis[j] && (x == 0 || vis[x]) {
  				ans += dfs(j, cnt+1)
  			}
  		}
  		vis[i] = false
  		return ans
  	}
  	return dfs(1, 1)*4 + dfs(2, 1)*4 + dfs(5, 1)
  }
  

• function numberOfPatterns(m: number, n: number): number {
      const cross: number[][] = Array(10)
          .fill(0)
          .map(() => Array(10).fill(0));
      const vis: boolean[] = Array(10).fill(false);
      cross[1][3] = cross[3][1] = 2;
      cross[1][7] = cross[7][1] = 4;
      cross[1][9] = cross[9][1] = 5;
      cross[2][8] = cross[8][2] = 5;
      cross[3][7] = cross[7][3] = 5;
      cross[3][9] = cross[9][3] = 6;
      cross[4][6] = cross[6][4] = 5;
      cross[7][9] = cross[9][7] = 8;
      const dfs = (i: number, cnt: number): number => {
          if (cnt > n) {
              return 0;
          }
          vis[i] = true;
          let ans = 0;
          if (cnt >= m) {
              ++ans;
          }
          for (let j = 1; j < 10; ++j) {
              const x = cross[i][j];
              if (!vis[j] && (x === 0 || vis[x])) {
                  ans += dfs(j, cnt + 1);
              }
          }
          vis[i] = false;
          return ans;
      };
      return dfs(1, 1) * 4 + dfs(2, 1) * 4 + dfs(5, 1);
  }
  
  

All Problems

All Solutions