Welcome to Subscribe On Youtube
Question
Formatted question description: https://leetcode.ca/all/337.html
The thief has found himself a new place for his thievery again. There is only one entrance to this area, called root.
Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if two directly-linked houses were broken into on the same night.
Given the root of the binary tree, return the maximum amount of money the thief can rob without alerting the police.
Example 1:
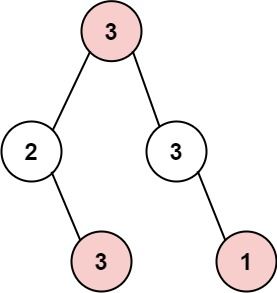
Input: root = [3,2,3,null,3,null,1] Output: 7 Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
Example 2:
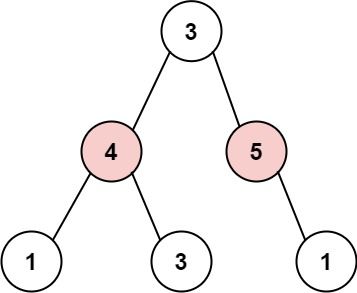
Input: root = [3,4,5,1,3,null,1] Output: 9 Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. 0 <= Node.val <= 104
Algorithm
Key Ideas:
- The solution uses a Depth-First Search (DFS) approach with memoization (caching) to efficiently calculate the maximum amount of money that can be robbed.
- It considers two scenarios at each node:
- The current node is robbed (
isCurrentRootRobbedisTrue). - The current node is not robbed (
isCurrentRootRobbedisFalse).
- The current node is robbed (
- The solution maximizes the total amount by choosing the best scenario at each node.
Detailed Explanation:
-
Base Case: If the current node (
root) isNone, the function returns 0 since there is no money to rob. - DFS with Two Scenarios:
- When
isCurrentRootRobbedisTrue, it means the current node is being robbed. Therefore, the children of the current node cannot be robbed due to the problem’s adjacency constraint. The total amount in this scenario is the value of the current node plus the optimal amounts from not robbing its left and right children. - When
isCurrentRootRobbedisFalse, it means the current node is not being robbed. Thus, the optimal amount from this node is the sum of the optimal amounts from either robbing or not robbing its left and right children. This is calculated by callingself.rob(root.left)andself.rob(root.right).
- When
- Memoization (@cache):
- The
@cachedecorator from Python’s functools library caches the results of expensive function calls and returns the cached result when the same inputs occur again. This significantly reduces the number of calculations by avoiding redundant DFS calls for the same subtree and scenario. - This memoization is crucial for the solution to meet the time constraints of the problem, as it prevents the exponential blow-up in runtime that would occur from recalculating the optimal robbery plan for each subtree multiple times.
- The
Note on a common-sense mistake on this question
The example given above seems to be stolen every other node, but in fact it is not necessarily only every other, such as the following example
4
/
1
/
2
/
3
If you steal one by every other node, then 4+2=6 or 1+3=4. In fact, the optimal solution should be 4+3=7, which is two times apart, so it is purely how to get it. Then this kind of problem is a typical recursive problem. Can be done using backtracking.
Code
-
public class House_Robber_III { /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution_singleRecursion { public int rob(TreeNode root) { return Math.max(dfs(root, true), dfs(root, false)); } private int dfs(TreeNode root, boolean isCurrentRootRobbed) { if (root == null) { return 0; } if (isCurrentRootRobbed) { return root.val + dfs(root.left, false) + dfs(root.right, false); } else { // child can be either rob or no-rob return Math.max(dfs(root.left, true), dfs(root.left, false)) + Math.max(dfs(root.right, true), dfs(root.right, false)); } } } class Solution { /* 1. node value can be negative? */ public int rob(TreeNode root) { if (root == null) { return 0; } return Math.max(target(root), skip(root)); } private int target(TreeNode root) { if (root == null) { return 0; } return root.val + skip(root.left) + skip(root.right); } private int skip(TreeNode root) { if (root == null) { return 0; } // @note: not target, but rob again => 因为理论上可以连续skip两层 // return target(root.left) + target(root.right); return rob(root.left) + rob(root.right); } } } ///////// /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private Map<TreeNode, Integer> memo; public int rob(TreeNode root) { memo = new HashMap<>(); return dfs(root); } private int dfs(TreeNode root) { if (root == null) { return 0; } if (memo.containsKey(root)) { return memo.get(root); } int a = dfs(root.left) + dfs(root.right); int b = root.val; if (root.left != null) { b += dfs(root.left.left) + dfs(root.left.right); } if (root.right != null) { b += dfs(root.right.left) + dfs(root.right.right); } int res = Math.max(a, b); memo.put(root, res); return res; } } -
// OJ: https://leetcode.com/problems/house-robber-iii/ // Time: O(N) // Space: O(H) class Solution { pair<int, int> dfs(TreeNode* root) { // rob, skip if (!root) return { 0, 0 }; auto [lr, ls] = dfs(root->left); auto [rr, rs] = dfs(root->right); return { root->val + ls + rs, max(lr, ls) + max(rr, rs) }; } public: int rob(TreeNode* root) { auto [r, s] = dfs(root); return max(r, s); } }; -
class Solution: def rob(self, root: TreeNode) -> int: return max(self.dfs(root, True), self.dfs(root, False)) # if no cache, then running time over limit @cache def dfs(self, root: TreeNode, isCurrentRootRobbed: bool) -> int: if not root: return 0 if isCurrentRootRobbed: return root.val + self.dfs(root.left, False) + self.dfs(root.right, False) else: return self.rob(root.left) + self.rob(root.right) # below else logic also passing OJ # return max(self.dfs(root.left, True), self.dfs(root.left, False)) + max(self.dfs(root.right, True), self.dfs(root.right, False)) ########### # better and concise class Solution: # post-order def rob(self, root: TreeNode) -> int: def dfs(node): if not node: return 0, 0 left, right = dfs(node.left), dfs(node.right) rob = node.val + left[1] + right[1] # [1] meaming left/right children skippted skip = max(left) + max(right) return rob, skip return max(dfs(root)) ########### class Solution: # return in else is too lengthy... def rob(self, root: TreeNode) -> int: return max(self.dfs(root, True), self.dfs(root, False)) # if no cache, then running time over limit @cache def dfs(self, root: TreeNode, isCurrentRootRobbed: bool) -> int: if not root: return 0 if isCurrentRootRobbed: return root.val + self.dfs(root.left, False) + self.dfs(root.right, False) else: return max(self.dfs(root.left, True), self.dfs(root.left, False)) + max(self.dfs(root.right, True), self.dfs(root.right, False)) -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func rob(root *TreeNode) int { memo := make(map[*TreeNode]int) var dfs func(root *TreeNode) int dfs = func(root *TreeNode) int { if root == nil { return 0 } if _, ok := memo[root]; ok { return memo[root] } a := dfs(root.Left) + dfs(root.Right) b := root.Val if root.Left != nil { b += dfs(root.Left.Left) + dfs(root.Left.Right) } if root.Right != nil { b += dfs(root.Right.Left) + dfs(root.Right.Right) } res := max(a, b) memo[root] = res return res } return dfs(root) } func max(a, b int) int { if a > b { return a } return b } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function rob(root: TreeNode | null): number { const dfs = (root: TreeNode | null): [number, number] => { if (!root) { return [0, 0]; } const [la, lb] = dfs(root.left); const [ra, rb] = dfs(root.right); return [root.val + lb + rb, Math.max(la, lb) + Math.max(ra, rb)]; }; return Math.max(...dfs(root)); }