331. Verify Preorder Serialization of a Binary Tree

Description

One way to serialize a binary tree is to use preorder traversal. When we encounter a non-null node, we record the node's value. If it is a null node, we record using a sentinel value such as '#'.

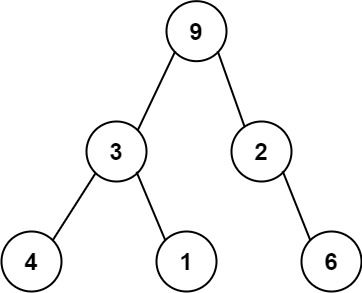
For example, the above binary tree can be serialized to the string "9,3,4,#,#,1,#,#,2,#,6,#,#", where '#' represents a null node.

Given a string of comma-separated values preorder, return true if it is a correct preorder traversal serialization of a binary tree.

It is guaranteed that each comma-separated value in the string must be either an integer or a character '#' representing null pointer.

You may assume that the input format is always valid.

For example, it could never contain two consecutive commas, such as "1,,3".

Note: You are not allowed to reconstruct the tree.

Example 1:

Input: preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#"
Output: true

Example 2:

Input: preorder = "1,#"
Output: false

Example 3:

Input: preorder = "9,#,#,1"
Output: false

Constraints:

1 <= preorder.length <= 10⁴
preorder consist of integers in the range [0, 100] and '#' separated by commas ','.

Solutions

In a valid binary tree serialization, each non-null node is followed by two child nodes, which may themselves be null ('#') to indicate the absence of a child node.

Core Logic

The algorithm is based on the concept of indegree and outdegree. Each node in a binary tree (except the root) has 1 indegree (an edge from its parent) and 2 outdegrees (edges to its children, if non-null). The root node is unique because it does not have a parent, so it starts with an indegree of 1 less than usual to balance this out.

Initialization:
- The preorder string is split by commas into a list of nodes, where each element represents a node in the tree. A node can either be a non-null value or '#' for a null node.
- Initialize indegree to 1, accounting for the root node which doesn’t have a parent.
Iterating Through Nodes:
- For each node in the serialized tree, decrease indegree by 1, reflecting that one node (either null or non-null) has been processed.
- If at any point indegree becomes negative, the function returns False. This is because a negative indegree indicates there are more edges pointing to nodes than there are nodes available, implying the serialization cannot represent a valid binary tree.
- If the node is not null (node != '#'), increase indegree by 2, accounting for the two children that a non-null node is supposed to have.
Validation:
- After processing all nodes, if the final indegree is 0, it indicates that the serialization could potentially represent a valid binary tree, where all nodes have the correct number of incoming and outgoing edges. Therefore, the function returns True.
- If indegree is not 0, the serialization does not correctly represent a binary tree, and the function returns False.

Example

Consider the serialization preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#":

Start with indegree = 1 for the root.
Process each node, adjusting indegree accordingly. Non-null nodes increase indegree by 2 (for their children), while processing any node (null or non-null) decreases indegree by 1.
The serialization ends with indegree = 0, indicating it is a valid binary tree serialization.

class Solution {
    public boolean isValidSerialization(String preorder) {
        List<String> stk = new ArrayList<>();
        for (String s : preorder.split(",")) {
            stk.add(s);
            while (stk.size() >= 3 && stk.get(stk.size() - 1).equals("#")
                && stk.get(stk.size() - 2).equals("#") && !stk.get(stk.size() - 3).equals("#")) {
                stk.remove(stk.size() - 1);
                stk.remove(stk.size() - 1);
                stk.remove(stk.size() - 1);
                stk.add("#");
            }
        }
        return stk.size() == 1 && stk.get(0).equals("#");
    }
}

class Solution {
public:
    bool isValidSerialization(string preorder) {
        vector<string> stk;
        stringstream ss(preorder);
        string s;
        while (getline(ss, s, ',')) {
            stk.push_back(s);
            while (stk.size() >= 3 && stk[stk.size() - 1] == "#" && stk[stk.size() - 2] == "#" && stk[stk.size() - 3] != "#") {
                stk.pop_back();
                stk.pop_back();
                stk.pop_back();
                stk.push_back("#");
            }
        }
        return stk.size() == 1 && stk[0] == "#";
    }
};

'''
In this solution, we split the input string by comma to get a list of nodes. 
We then initialize the indegree counter to 1 for the root node, 
since the root has no incoming edges.

We then loop through the nodes and for each node, we decrease the indegree counter by 1. 
If the indegree counter becomes negative, 
it means that there are more incoming edges than expected, 
and the tree is invalid. In this case, we return False.

If the current node is not null (i.e., not '#'), 
we increase the indegree counter by 2 for its two children. 
This is because every non-null node has two children in a binary tree. 
Finally, we return True if the final indegree counter is 0, 
meaning that all incoming edges have been accounted for.
'''
class Solution:
    def isValidSerialization(self, preorder: str) -> bool:
        # Split the string by comma to get the list of nodes
        nodes = preorder.split(',')

        # since the root has no incoming edges
        indegree = 1

        for node in nodes:
            # Decrease the indegree for the current node
            indegree -= 1

            # If the indegree is negative, return False because the tree is invalid
            if indegree < 0:
                return False

            # If the current node is not null, increase the indegree by 2 for its children
            if node != '#':
                indegree += 2

        # Return True if the final indegree is 0
        return indegree == 0

############

class Solution:
    def isValidSerialization(self, preorder: str) -> bool:
        if not preorder:
            return True
        
        nodes = preorder.split(",")
        stack = []
        
        for node in nodes:
            if node == "#":
                # after first while loop, current node can be deemed as #
                while stack and stack[-1] == "#":
                    stack.pop() # pop # in stack
                    if not stack: # should leave a number in stack
                        return False
                    
                    stack.pop() # pop val with left-# and right-#   =>   repalce it with #
            stack.append(node)
        
        return len(stack) == 1 and stack[0] == "#"

############

class Solution:
    def isValidSerialization(self, preorder: str) -> bool:
        stk = []
        for c in preorder.split(","):
            stk.append(c)
            while len(stk) > 2 and stk[-1] == stk[-2] == "#" and stk[-3] != "#":
                stk = stk[:-3]
                stk.append("#")
        return len(stk) == 1 and stk[0] == "#"

func isValidSerialization(preorder string) bool {
	stk := []string{}
	for _, s := range strings.Split(preorder, ",") {
		stk = append(stk, s)
		for len(stk) >= 3 && stk[len(stk)-1] == "#" && stk[len(stk)-2] == "#" && stk[len(stk)-3] != "#" {
			stk = stk[:len(stk)-3]
			stk = append(stk, "#")
		}
	}
	return len(stk) == 1 && stk[0] == "#"
}

function isValidSerialization(preorder: string): boolean {
    const stk: string[] = [];
    for (const s of preorder.split(',')) {
        stk.push(s);
        while (stk.length >= 3 && stk.at(-1) === '#' && stk.at(-2) === '#' && stk.at(-3) !== '#') {
            stk.splice(-3, 3, '#');
        }
    }
    return stk.length === 1 && stk[0] === '#';
}

331 - Verify Preorder Serialization of a Binary Tree

331. Verify Preorder Serialization of a Binary Tree

Description

Solutions

Core Logic

Example

All Problems

All Solutions

Welcome to Subscribe On Youtube

331. Verify Preorder Serialization of a Binary Tree

Description

Solutions

Core Logic

Example

All Problems

All Solutions