Welcome to Subscribe On Youtube

319. Bulb Switcher

Description

There are n bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.

On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb.

Return the number of bulbs that are on after n rounds.

 

Example 1:

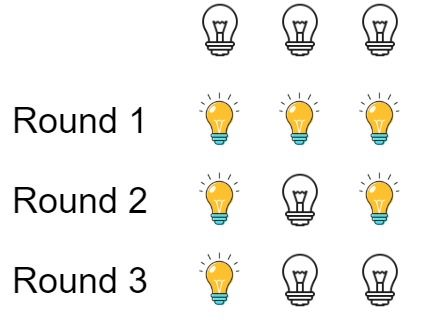
Input: n = 3
Output: 1
Explanation: At first, the three bulbs are [off, off, off].
After the first round, the three bulbs are [on, on, on].
After the second round, the three bulbs are [on, off, on].
After the third round, the three bulbs are [on, off, off]. 
So you should return 1 because there is only one bulb is on.

Example 2:

Input: n = 0
Output: 0

Example 3:

Input: n = 1
Output: 1

 

Constraints:

  • 0 <= n <= 109

Solutions

  • class Solution {
    public int bulbSwitch(int n) {
        return (int) Math.sqrt(n);
    }
}


  • class Solution:
    def bulbSwitch(self, n: int) -> int:
        return int(n ** (1 / 2))


  • class Solution {
public:
    int bulbSwitch(int n) {
        return (int) sqrt(n);
    }
};

  • func bulbSwitch(n int) int {
	return int(math.Sqrt(float64(n)))
}

  • function bulbSwitch(n: number): number {
    return Math.floor(Math.sqrt(n));
}

All Problems

All Solutions