Welcome to Subscribe On Youtube
317. Shortest Distance from All Buildings
Description
You are given an m x n grid grid of values 0, 1, or 2, where:
- each
0marks an empty land that you can pass by freely, - each
1marks a building that you cannot pass through, and - each
2marks an obstacle that you cannot pass through.
You want to build a house on an empty land that reaches all buildings in the shortest total travel distance. You can only move up, down, left, and right.
Return the shortest travel distance for such a house. If it is not possible to build such a house according to the above rules, return -1.
The total travel distance is the sum of the distances between the houses of the friends and the meeting point.
The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.
Example 1:
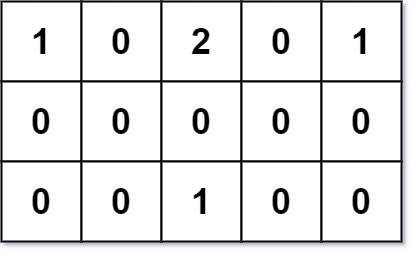
Input: grid = [[1,0,2,0,1],[0,0,0,0,0],[0,0,1,0,0]] Output: 7 Explanation: Given three buildings at (0,0), (0,4), (2,2), and an obstacle at (0,2). The point (1,2) is an ideal empty land to build a house, as the total travel distance of 3+3+1=7 is minimal. So return 7.
Example 2:
Input: grid = [[1,0]] Output: 1
Example 3:
Input: grid = [[1]] Output: -1
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 50grid[i][j]is either0,1, or2.- There will be at least one building in the
grid.
Solutions
This solution code defines a method to find the shortest distance from a “free land” (represented as 0) to all buildings (1) in a given 2D grid. The distance is the sum of the shortest paths from the free land to all buildings. The method aims to find the minimum of these sums for all free lands in the grid. It returns -1 if it’s not possible for a free land to reach every building.
How It Works
-
Initialization: The dimensions of the grid (
mandn) are determined. A queueqis initialized for Breadth-First Search (BFS),totalcounts the number of buildings,cnttracks how many buildings can be reached from each cell, anddiststores the total distance from a free land to all reachable buildings. - Building BFS Traversal: The grid is traversed to find buildings (
grid[i][j] == 1). For each building found, BFS is performed to calculate its distance to all reachable free lands. During this process:totalis incremented for each building found.- A
vis(visited) set is used to avoid revisiting cells within the same BFS traversal. - The BFS increments the distance (
d) as it moves away from the building, updatingdist[x][y]with the distance to reach the free land at(x, y)from the current building. - It also increments
cnt[x][y]indicating that another building can reach this free land.
-
Finding the Optimal Free Land: After BFS for all buildings, the grid is traversed again to find a free land (
grid[i][j] == 0) from which the total number of reachable buildings (cnt[i][j]) equals the total number of buildings. Among these free lands, it looks for the one with the minimum total distance to all buildings (dist[i][j]). - Returning the Result: If such a free land exists, the minimum total distance (
ans) is returned. If no such free land exists (meaningansremainsinf), it returns-1, indicating that no free land can reach all buildings.
Example
Consider the grid:
1 0 2 0 1
0 0 0 0 0
0 0 1 0 0
1represents buildings,2represents obstacles, and0represents free lands.- The algorithm performs BFS from each building to calculate distances to all reachable free lands and counts how many buildings each free land can reach.
- It then selects the free land that can reach all buildings with the minimum total distance sum.
Key Points
- The algorithm efficiently uses BFS from buildings rather than free lands, which reduces the number of BFS traversals required (since buildings are typically fewer than free lands).
- By keeping track of the number of buildings each free land can reach (
cnt) and the sum of distances (dist), the algorithm ensures that the selected free land can reach every building and does so with the shortest total distance. - The method is robust and accounts for cases where not all buildings are reachable from a free land, returning
-1in such scenarios.
-
class Solution { public int shortestDistance(int[][] grid) { int m = grid.length; int n = grid[0].length; Deque<int[]> q = new LinkedList<>(); int total = 0; int[][] cnt = new int[m][n]; int[][] dist = new int[m][n]; int[] dirs = {-1, 0, 1, 0, -1}; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (grid[i][j] == 1) { ++total; q.offer(new int[] {i, j}); int d = 0; boolean[][] vis = new boolean[m][n]; while (!q.isEmpty()) { ++d; for (int k = q.size(); k > 0; --k) { int[] p = q.poll(); for (int l = 0; l < 4; ++l) { int x = p[0] + dirs[l]; int y = p[1] + dirs[l + 1]; if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 0 && !vis[x][y]) { ++cnt[x][y]; dist[x][y] += d; q.offer(new int[] {x, y}); vis[x][y] = true; } } } } } } } int ans = Integer.MAX_VALUE; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (grid[i][j] == 0 && cnt[i][j] == total) { ans = Math.min(ans, dist[i][j]); } } } return ans == Integer.MAX_VALUE ? -1 : ans; } } -
class Solution { public: int shortestDistance(vector<vector<int>>& grid) { int m = grid.size(); int n = grid[0].size(); typedef pair<int, int> pii; queue<pii> q; int total = 0; vector<vector<int>> cnt(m, vector<int>(n)); vector<vector<int>> dist(m, vector<int>(n)); vector<int> dirs = {-1, 0, 1, 0, -1}; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (grid[i][j] == 1) { ++total; q.push({i, j}); vector<vector<bool>> vis(m, vector<bool>(n)); int d = 0; while (!q.empty()) { ++d; for (int k = q.size(); k > 0; --k) { auto p = q.front(); q.pop(); for (int l = 0; l < 4; ++l) { int x = p.first + dirs[l]; int y = p.second + dirs[l + 1]; if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 0 && !vis[x][y]) { ++cnt[x][y]; dist[x][y] += d; q.push({x, y}); vis[x][y] = true; } } } } } } } int ans = INT_MAX; for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) if (grid[i][j] == 0 && cnt[i][j] == total) ans = min(ans, dist[i][j]); return ans == INT_MAX ? -1 : ans; } }; -
class Solution: def shortestDistance(self, grid: List[List[int]]) -> int: m, n = len(grid), len(grid[0]) q = deque() total = 0 # total building count # cnt: how many buildings can reach (x,y) # if there is a column all blockers, then (x,y) cannot reach every building cnt = [[0] * n for _ in range(m)] dist = [[0] * n for _ in range(m)] for i in range(m): for j in range(n): if grid[i][j] == 1: total += 1 q.append((i, j)) d = 0 vis = set() # reset for every free-land while q: d += 1 for _ in range(len(q)): r, c = q.popleft() for a, b in [[0, 1], [0, -1], [1, 0], [-1, 0]]: x, y = r + a, c + b if ( 0 <= x < m and 0 <= y < n and grid[x][y] == 0 and (x, y) not in vis ): cnt[x][y] += 1 dist[x][y] += d q.append((x, y)) vis.add((x, y)) ans = inf for i in range(m): for j in range(n): if grid[i][j] == 0 and cnt[i][j] == total: ans = min(ans, dist[i][j]) return -1 if ans == inf else ans -
func shortestDistance(grid [][]int) int { m, n := len(grid), len(grid[0]) var q [][]int total := 0 cnt := make([][]int, m) dist := make([][]int, m) for i := range cnt { cnt[i] = make([]int, n) dist[i] = make([]int, n) } dirs := []int{-1, 0, 1, 0, -1} for i := 0; i < m; i++ { for j := 0; j < n; j++ { if grid[i][j] == 1 { total++ q = append(q, []int{i, j}) vis := make([]bool, m*n) d := 0 for len(q) > 0 { d++ for k := len(q); k > 0; k-- { p := q[0] q = q[1:] for l := 0; l < 4; l++ { x, y := p[0]+dirs[l], p[1]+dirs[l+1] if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 0 && !vis[x*n+y] { cnt[x][y]++ dist[x][y] += d q = append(q, []int{x, y}) vis[x*n+y] = true } } } } } } } ans := math.MaxInt32 for i := 0; i < m; i++ { for j := 0; j < n; j++ { if grid[i][j] == 0 && cnt[i][j] == total { if ans > dist[i][j] { ans = dist[i][j] } } } } if ans == math.MaxInt32 { return -1 } return ans }