Welcome to Subscribe On Youtube
314. Binary Tree Vertical Order Traversal
Description
Given the root of a binary tree, return the vertical order traversal of its nodes' values. (i.e., from top to bottom, column by column).
If two nodes are in the same row and column, the order should be from left to right.
Example 1:
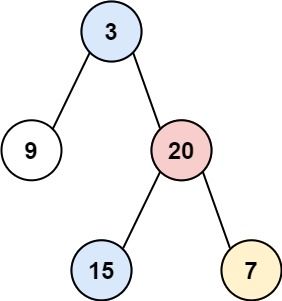
Input: root = [3,9,20,null,null,15,7] Output: [[9],[3,15],[20],[7]]
Example 2:
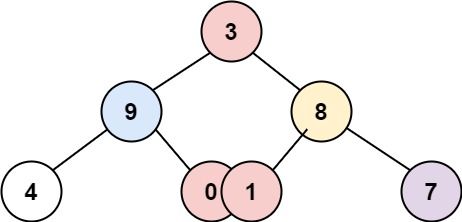
Input: root = [3,9,8,4,0,1,7] Output: [[4],[9],[3,0,1],[8],[7]]
Example 3:
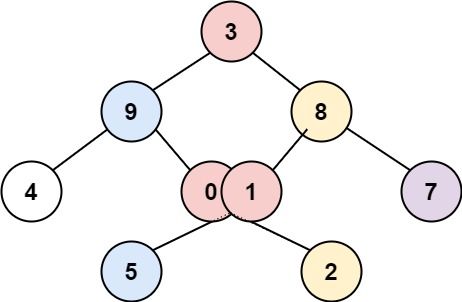
Input: root = [3,9,8,4,0,1,7,null,null,null,2,5] Output: [[4],[9,5],[3,0,1],[8,2],[7]]
Constraints:
- The number of nodes in the tree is in the range
[0, 100]. -100 <= Node.val <= 100
Solutions
Solution 1: DFS
DFS traverses the binary tree, recording the value, depth, and horizontal offset of each node. Then sort all nodes by horizontal offset from small to large, then by depth from small to large, and finally group by horizontal offset.
The time complexity is $O(n\log n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes in the binary tree.
Solution 2: BFS
A better approach to this problem should be BFS, traversing from top to bottom level by level.
The time complexity is $O(n\log n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes in the binary tree.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public List<List<Integer>> verticalOrder(TreeNode root) { List<List<Integer>> ans = new ArrayList<>(); if (root == null) { return ans; } Deque<Pair<TreeNode, Integer>> q = new ArrayDeque<>(); q.offer(new Pair<>(root, 0)); TreeMap<Integer, List<Integer>> d = new TreeMap<>(); while (!q.isEmpty()) { for (int n = q.size(); n > 0; --n) { var p = q.pollFirst(); root = p.getKey(); int offset = p.getValue(); d.computeIfAbsent(offset, k -> new ArrayList()).add(root.val); if (root.left != null) { q.offer(new Pair<>(root.left, offset - 1)); } if (root.right != null) { q.offer(new Pair<>(root.right, offset + 1)); } } } return new ArrayList<>(d.values()); } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: vector<vector<int>> verticalOrder(TreeNode* root) { vector<vector<int>> ans; if (!root) return ans; map<int, vector<int>> d; queue<pair<TreeNode*, int>> q{ { {root, 0} } }; while (!q.empty()) { for (int n = q.size(); n; --n) { auto p = q.front(); q.pop(); root = p.first; int offset = p.second; d[offset].push_back(root->val); if (root->left) q.push({root->left, offset - 1}); if (root->right) q.push({root->right, offset + 1}); } } for (auto& [_, v] : d) { ans.push_back(v); } return ans; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right ''' >>> d = {1:'a', -1:'b', 10:'c', -100:'d'} >>> >>> d.items() {1: 'a', 10: 'c', -100: 'd', -1: 'b'} >>> ds = sorted(d.items()) >>> ds [(-100, 'd'), (-1, 'b'), (1, 'a'), (10, 'c')] >>> sorted(d.items(), key=lambda l: l[1]) [(1, 'a'), (-1, 'b'), (10, 'c'), (-100, 'd')] >>> dict(sorted(d.items(), key=lambda l: l[1])) {1: 'a', 10: 'c', -100: 'd', -1: 'b'} >>> [v for i,v in sorted(d.items(), key=lambda l: l[0])] ['d', 'b', 'a', 'c'] ''' class Solution: def verticalOrder(self, root: Optional[TreeNode]) -> List[List[int]]: if root is None: return [] q = deque([(root, 0)]) d = defaultdict(list) while q: for _ in range(len(q)): root, offset = q.popleft() d[offset].append(root.val) if root.left: q.append((root.left, offset - 1)) if root.right: q.append((root.right, offset + 1)) return [v for _, v in sorted(d.items())] ############### from sortedcontainers import SortedDict from typing import List from collections import deque # similar to above, but use existing data structure class Solution: def verticalOrder(self, root: TreeNode) -> List[List[int]]: if not root: return [] # Use SortedDict to automatically sort by column index sorted_dict = SortedDict() # Queue for breadth-first search; stores pairs of (node, column_index) queue = deque([(0, root)]) while queue: node, column = queue.popleft() if column not in sorted_dict: sorted_dict[column] = [node.val] else: sorted_dict[column].append(node.val) # Add left and right children to the queue if node.left: queue.append((node.left, column - 1)) if node.right: queue.append((node.right, column + 1)) # Return the values from sorted_dict as a list of lists return list(sorted_dict.values()) ########### # another SortedDict, but different handling on None node, before enqueue vs after enqueue class Solution: def verticalOrder(self, root: TreeNode): if not root: return [] # Initialize a SortedDict to maintain columns in sorted order. column_table = SortedDict() queue = deque([(root, 0)]) # (node, column_index) while queue: node, column = queue.popleft() if node is not None: if column not in column_table: column_table[column] = [] column_table[column].append(node.val) # Add left and right children to the queue. queue.append((node.left, column - 1)) queue.append((node.right, column + 1)) # Extract the values from the sorted dictionary and return them. return list(column_table.values()) ################# from collections import defaultdict class Solution(object): def verticalOrder(self, root): """ :type root: TreeNode :rtype: List[List[int]] """ def dfs(p, i, j, res): # i -> depth, j -> vertical-shift if p: res[j].append((p.val, i)) self.leftMost = min(j, self.leftMost) dfs(p.left, i + 1, j - 1, res) dfs(p.right, i + 1, j + 1, res) self.leftMost = float("inf") ans = [] res = defaultdict(list) dfs(root, 0, 0, res) i = self.leftMost while True: if not res[i]: break ans.append([item[0] for item in sorted(res[i], key=lambda a: a[1])]) i += 1 return ans -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func verticalOrder(root *TreeNode) [][]int { ans := [][]int{} if root == nil { return ans } d := map[int][]int{} q := []pair{pair{root, 0} } for len(q) > 0 { for n := len(q); n > 0; n-- { p := q[0] q = q[1:] root = p.node offset := p.offset d[offset] = append(d[offset], root.Val) if root.Left != nil { q = append(q, pair{root.Left, offset - 1}) } if root.Right != nil { q = append(q, pair{root.Right, offset + 1}) } } } idx := []int{} for i := range d { idx = append(idx, i) } sort.Ints(idx) for _, i := range idx { ans = append(ans, d[i]) } return ans } type pair struct { node *TreeNode offset int }