Welcome to Subscribe On Youtube

308. Range Sum Query 2D - Mutable

Description

Given a 2D matrix matrix, handle multiple queries of the following types:

  1. Update the value of a cell in matrix.
  2. Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

  • NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
  • void update(int row, int col, int val) Updates the value of matrix[row][col] to be val.
  • int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

 

Example 1:

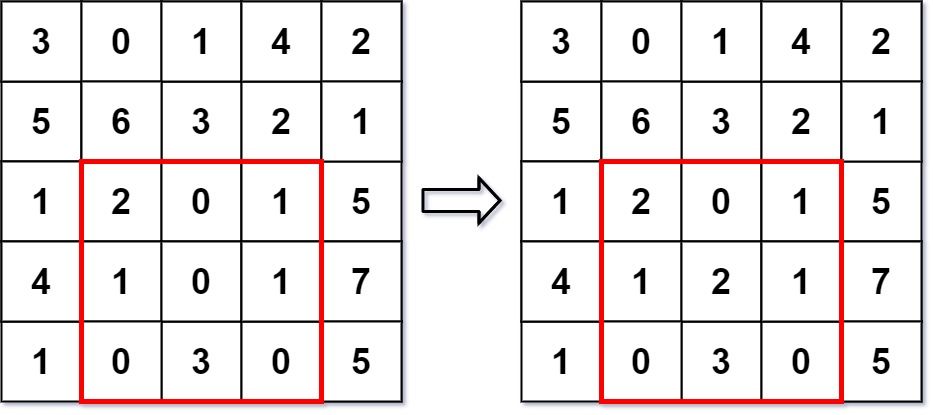
Input
["NumMatrix", "sumRegion", "update", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [3, 2, 2], [2, 1, 4, 3]]
Output
[null, 8, null, 10]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e. sum of the left red rectangle)
numMatrix.update(3, 2, 2); // matrix changes from left image to right image
numMatrix.sumRegion(2, 1, 4, 3); // return 10 (i.e. sum of the right red rectangle)

 

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 200
  • -1000 <= matrix[i][j] <= 1000
  • 0 <= row < m
  • 0 <= col < n
  • -1000 <= val <= 1000
  • 0 <= row1 <= row2 < m
  • 0 <= col1 <= col2 < n
  • At most 5000 calls will be made to sumRegion and update.

Solutions

Solution 1

Binary Indexed Tree or Segment Tree.

In the class NumMatrix, maintain the original matrix matrix and maintain another 2D array rowSums that has the same size as matrix and stores the sums of the elements to the left in the same row. Concretely, rowSums[i][j] is the sum of all elements from matrix[i][0] to matrix[i][j]. Also maintain rows and columns of matrix as well.

For the constructor, initialize the original matrix matrix, the 2D array rowSums, and rows and columns.

For update, calculate difference = val - matrix[row][column], update matrix[row][col] = val, and for col <= i < columns, update rowSums[row][i] += difference.

For sumRegion, if row1 > row2 or col1 > col2, then the region is invalid, so return 0. Otherwise, for each row from row1 to row2, calculate the sum of elements from column col1 to column col2. The sum in row row and columns range [col1, col2] is calculated as rowSums[row][col2] for col1 == 0, or rowSums[row][col2] - rowSums[row][col1 - 1] for col1 > 0.

Solution 2

The line segment tree divides the entire interval into multiple discontinuous sub-intervals, and the number of sub-intervals does not exceed log(width). To update the value of an element, you only need to update log(width) intervals, and these intervals are all included in a large interval containing the element.

  • Each node of the line segment tree represents an interval;
  • The line segment tree has a unique root node, and the interval represented is the entire statistical range, such as [1, N];
  • Each leaf node of the line segment tree represents a meta-interval [x, x] of length 1;
  • For each internal node [l, r], its left son is [l, mid] and its right son is [mid + 1, r], where mid = ⌊(l + r) / 2⌋ (that is, rounded down).
  • class BinaryIndexedTree {
    private int n;
    private int[] c;

    public BinaryIndexedTree(int n) {
        this.n = n;
        c = new int[n + 1];
    }

    public void update(int x, int delta) {
        while (x <= n) {
            c[x] += delta;
            x += lowbit(x);
        }
    }

    public int query(int x) {
        int s = 0;
        while (x > 0) {
            s += c[x];
            x -= lowbit(x);
        }
        return s;
    }

    public static int lowbit(int x) {
        return x & -x;
    }
}

class NumMatrix {
    private BinaryIndexedTree[] trees;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        trees = new BinaryIndexedTree[m];
        for (int i = 0; i < m; ++i) {
            BinaryIndexedTree tree = new BinaryIndexedTree(n);
            for (int j = 0; j < n; ++j) {
                tree.update(j + 1, matrix[i][j]);
            }
            trees[i] = tree;
        }
    }

    public void update(int row, int col, int val) {
        BinaryIndexedTree tree = trees[row];
        int prev = tree.query(col + 1) - tree.query(col);
        tree.update(col + 1, val - prev);
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int s = 0;
        for (int i = row1; i <= row2; ++i) {
            BinaryIndexedTree tree = trees[i];
            s += tree.query(col2 + 1) - tree.query(col1);
        }
        return s;
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * obj.update(row,col,val);
 * int param_2 = obj.sumRegion(row1,col1,row2,col2);
 */


// Solution 2
class Node {
    int l;
    int r;
    int v;
}

class SegmentTree {
    private Node[] tr;
    private int[] nums;

    public SegmentTree(int[] nums) {
        int n = nums.length;
        tr = new Node[n << 2];
        this.nums = nums;
        for (int i = 0; i < tr.length; ++i) {
            tr[i] = new Node();
        }
        build(1, 1, n);
    }

    public void build(int u, int l, int r) {
        tr[u].l = l;
        tr[u].r = r;
        if (l == r) {
            tr[u].v = nums[l - 1];
            return;
        }
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }

    public void modify(int u, int x, int v) {
        if (tr[u].l == x && tr[u].r == x) {
            tr[u].v = v;
            return;
        }
        int mid = (tr[u].l + tr[u].r) >> 1;
        if (x <= mid) {
            modify(u << 1, x, v);
        } else {
            modify(u << 1 | 1, x, v);
        }
        pushup(u);
    }

    public void pushup(int u) {
        tr[u].v = tr[u << 1].v + tr[u << 1 | 1].v;
    }

    public int query(int u, int l, int r) {
        if (tr[u].l >= l && tr[u].r <= r) {
            return tr[u].v;
        }
        int mid = (tr[u].l + tr[u].r) >> 1;
        int v = 0;
        if (l <= mid) {
            v += query(u << 1, l, r);
        }
        if (r > mid) {
            v += query(u << 1 | 1, l, r);
        }
        return v;
    }
}

class NumMatrix {
    private SegmentTree[] trees;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        trees = new SegmentTree[m];
        for (int i = 0; i < m; ++i) {
            trees[i] = new SegmentTree(matrix[i]);
        }
    }

    public void update(int row, int col, int val) {
        SegmentTree tree = trees[row];
        tree.modify(1, col + 1, val);
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int s = 0;
        for (int row = row1; row <= row2; ++row) {
            SegmentTree tree = trees[row];
            s += tree.query(1, col1 + 1, col2 + 1);
        }
        return s;
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * obj.update(row,col,val);
 * int param_2 = obj.sumRegion(row1,col1,row2,col2);
 */


  • class BinaryIndexedTree {
public:
    int n;
    vector<int> c;

    BinaryIndexedTree(int _n)
        : n(_n)
        , c(_n + 1) {}

    void update(int x, int delta) {
        while (x <= n) {
            c[x] += delta;
            x += lowbit(x);
        }
    }

    int query(int x) {
        int s = 0;
        while (x > 0) {
            s += c[x];
            x -= lowbit(x);
        }
        return s;
    }

    int lowbit(int x) {
        return x & -x;
    }
};

class NumMatrix {
public:
    vector<BinaryIndexedTree*> trees;

    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        trees.resize(m);
        for (int i = 0; i < m; ++i) {
            BinaryIndexedTree* tree = new BinaryIndexedTree(n);
            for (int j = 0; j < n; ++j) tree->update(j + 1, matrix[i][j]);
            trees[i] = tree;
        }
    }

    void update(int row, int col, int val) {
        BinaryIndexedTree* tree = trees[row];
        int prev = tree->query(col + 1) - tree->query(col);
        tree->update(col + 1, val - prev);
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        int s = 0;
        for (int i = row1; i <= row2; ++i) {
            BinaryIndexedTree* tree = trees[i];
            s += tree->query(col2 + 1) - tree->query(col1);
        }
        return s;
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * obj->update(row,col,val);
 * int param_2 = obj->sumRegion(row1,col1,row2,col2);
 */


// Solution 2
class Node {
public:
    int l;
    int r;
    int v;
};

class SegmentTree {
public:
    vector<Node*> tr;
    vector<int> nums;

    SegmentTree(vector<int>& nums) {
        int n = nums.size();
        tr.resize(n << 2);
        this->nums = nums;
        for (int i = 0; i < tr.size(); ++i) tr[i] = new Node();
        build(1, 1, n);
    }

    void build(int u, int l, int r) {
        tr[u]->l = l;
        tr[u]->r = r;
        if (l == r) {
            tr[u]->v = nums[l - 1];
            return;
        }
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }

    void modify(int u, int x, int v) {
        if (tr[u]->l == x && tr[u]->r == x) {
            tr[u]->v = v;
            return;
        }
        int mid = (tr[u]->l + tr[u]->r) >> 1;
        if (x <= mid)
            modify(u << 1, x, v);
        else
            modify(u << 1 | 1, x, v);
        pushup(u);
    }

    int query(int u, int l, int r) {
        if (tr[u]->l >= l && tr[u]->r <= r) return tr[u]->v;
        int mid = (tr[u]->l + tr[u]->r) >> 1;
        int v = 0;
        if (l <= mid) v += query(u << 1, l, r);
        if (r > mid) v += query(u << 1 | 1, l, r);
        return v;
    }

    void pushup(int u) {
        tr[u]->v = tr[u << 1]->v + tr[u << 1 | 1]->v;
    }
};

class NumMatrix {
public:
    vector<SegmentTree*> trees;

    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        trees.resize(m);
        for (int i = 0; i < m; ++i) trees[i] = new SegmentTree(matrix[i]);
    }

    void update(int row, int col, int val) {
        SegmentTree* tree = trees[row];
        tree->modify(1, col + 1, val);
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        int s = 0;
        for (int row = row1; row <= row2; ++row) s += trees[row]->query(1, col1 + 1, col2 + 1);
        return s;
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * obj->update(row,col,val);
 * int param_2 = obj->sumRegion(row1,col1,row2,col2);
 */


  • # segment tree
class Node:
    def __init__(self):
        self.l = 0
        self.r = 0
        self.v = 0

class SegmentTree:
    def __init__(self, nums):
        n = len(nums)
        self.nums = nums
        self.tr = [Node() for _ in range(4 * n)]
        self.build(1, 1, n)

    def build(self, u, l, r):
        self.tr[u].l = l
        self.tr[u].r = r
        if l == r:
            self.tr[u].v = self.nums[l - 1]
            return
        mid = (l + r) >> 1
        self.build(u << 1, l, mid)
        self.build(u << 1 | 1, mid + 1, r)
        self.pushup(u)

    def modify(self, u, x, v):
        if self.tr[u].l == x and self.tr[u].r == x:
            self.tr[u].v = v
            return
        mid = (self.tr[u].l + self.tr[u].r) >> 1
        if x <= mid:
            self.modify(u << 1, x, v)
        else:
            self.modify(u << 1 | 1, x, v)
        self.pushup(u)

    def query(self, u, l, r):
        if self.tr[u].l >= l and self.tr[u].r <= r:
            return self.tr[u].v
        mid = (self.tr[u].l + self.tr[u].r) >> 1
        v = 0
        if l <= mid:
            v += self.query(u << 1, l, r)
        if r > mid:
            v += self.query(u << 1 | 1, l, r)
        return v

    def pushup(self, u):
        self.tr[u].v = self.tr[u << 1].v + self.tr[u << 1 | 1].v

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        self.trees = [SegmentTree(row) for row in matrix]

    def update(self, row: int, col: int, val: int) -> None:
        tree = self.trees[row]
        tree.modify(1, col + 1, val)

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return sum(self.trees[row].query(1, col1 + 1, col2 + 1) for row in range(row1, row2 + 1))


# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# obj.update(row,col,val)
# param_2 = obj.sumRegion(row1,col1,row2,col2)

############
'''
It uses a binary indexed tree (BIT) or Fenwick tree to efficiently update and query sums of submatrices.
The NumMatrix class constructor initializes the BIT and matrix data structure. 
The update method updates the matrix and BIT with the difference in values. 
The sumRegion method computes the sum of a submatrix using prefix sums computed with the BIT. 
The sum method computes a prefix sum in the BIT.


"Fenwick tree" vs "Segment tree"
https://stackoverflow.com/questions/64190332/fenwick-tree-vs-segment-tree

'''

class NumMatrix:
    def __init__(self, matrix: List[List[int]]):
        if not matrix or not matrix[0]:
            self.m, self.n = 0, 0
            return

        self.m, self.n = len(matrix), len(matrix[0])
        self.bit = [[0] * (self.n + 1) for _ in range(self.m + 1)]
        self.matrix = [[0] * self.n for _ in range(self.m)]
        
        for i in range(self.m):
            for j in range(self.n):
                self.update(i, j, matrix[i][j])

    def update(self, row: int, col: int, val: int) -> None:
        diff = val - self.matrix[row][col]
        self.matrix[row][col] = val
        i = row + 1
        while i <= self.m:
            j = col + 1
            while j <= self.n:
                self.bit[i][j] += diff
                j += j & -j
            i += i & -i

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return self.sum(row2 + 1, col2 + 1) - self.sum(row2 + 1, col1) - self.sum(row1, col2 + 1) + self.sum(row1, col1)

    def sum(self, row: int, col: int) -> int:
        res = 0
        i = row
        while i > 0:
            j = col
            while j > 0:
                res += self.bit[i][j]
                j -= j & -j
            i -= i & -i
        return res


# Solution 2
class Node:
    def __init__(self):
        self.l = 0
        self.r = 0
        self.v = 0


class SegmentTree:
    def __init__(self, nums):
        n = len(nums)
        self.nums = nums
        self.tr = [Node() for _ in range(4 * n)]
        self.build(1, 1, n)

    def build(self, u, l, r):
        self.tr[u].l = l
        self.tr[u].r = r
        if l == r:
            self.tr[u].v = self.nums[l - 1]
            return
        mid = (l + r) >> 1
        self.build(u << 1, l, mid)
        self.build(u << 1 | 1, mid + 1, r)
        self.pushup(u)

    def modify(self, u, x, v):
        if self.tr[u].l == x and self.tr[u].r == x:
            self.tr[u].v = v
            return
        mid = (self.tr[u].l + self.tr[u].r) >> 1
        if x <= mid:
            self.modify(u << 1, x, v)
        else:
            self.modify(u << 1 | 1, x, v)
        self.pushup(u)

    def query(self, u, l, r):
        if self.tr[u].l >= l and self.tr[u].r <= r:
            return self.tr[u].v
        mid = (self.tr[u].l + self.tr[u].r) >> 1
        v = 0
        if l <= mid:
            v += self.query(u << 1, l, r)
        if r > mid:
            v += self.query(u << 1 | 1, l, r)
        return v

    def pushup(self, u):
        self.tr[u].v = self.tr[u << 1].v + self.tr[u << 1 | 1].v


class NumMatrix:
    def __init__(self, matrix: List[List[int]]):
        self.trees = [SegmentTree(row) for row in matrix]

    def update(self, row: int, col: int, val: int) -> None:
        tree = self.trees[row]
        tree.modify(1, col + 1, val)

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return sum(
            self.trees[row].query(1, col1 + 1, col2 + 1)
            for row in range(row1, row2 + 1)
        )


# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# obj.update(row,col,val)
# param_2 = obj.sumRegion(row1,col1,row2,col2)


  • type BinaryIndexedTree struct {
	n int
	c []int
}

func newBinaryIndexedTree(n int) *BinaryIndexedTree {
	c := make([]int, n+1)
	return &BinaryIndexedTree{n, c}
}

func (this *BinaryIndexedTree) lowbit(x int) int {
	return x & -x
}

func (this *BinaryIndexedTree) update(x, delta int) {
	for x <= this.n {
		this.c[x] += delta
		x += this.lowbit(x)
	}
}

func (this *BinaryIndexedTree) query(x int) int {
	s := 0
	for x > 0 {
		s += this.c[x]
		x -= this.lowbit(x)
	}
	return s
}

type NumMatrix struct {
	trees []*BinaryIndexedTree
}

func Constructor(matrix [][]int) NumMatrix {
	n := len(matrix[0])
	var trees []*BinaryIndexedTree
	for _, row := range matrix {
		tree := newBinaryIndexedTree(n)
		for j, v := range row {
			tree.update(j+1, v)
		}
		trees = append(trees, tree)
	}
	return NumMatrix{trees}
}

func (this *NumMatrix) Update(row int, col int, val int) {
	tree := this.trees[row]
	prev := tree.query(col+1) - tree.query(col)
	tree.update(col+1, val-prev)
}

func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int {
	s := 0
	for i := row1; i <= row2; i++ {
		tree := this.trees[i]
		s += tree.query(col2+1) - tree.query(col1)
	}
	return s
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * obj := Constructor(matrix);
 * obj.Update(row,col,val);
 * param_2 := obj.SumRegion(row1,col1,row2,col2);
 */

All Problems

All Solutions