Welcome to Subscribe On Youtube
286. Walls and Gates
Description
You are given an m x n grid rooms initialized with these three possible values.
-1A wall or an obstacle.0A gate.INFInfinity means an empty room. We use the value231 - 1 = 2147483647to representINFas you may assume that the distance to a gate is less than2147483647.
Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with INF.
Example 1:
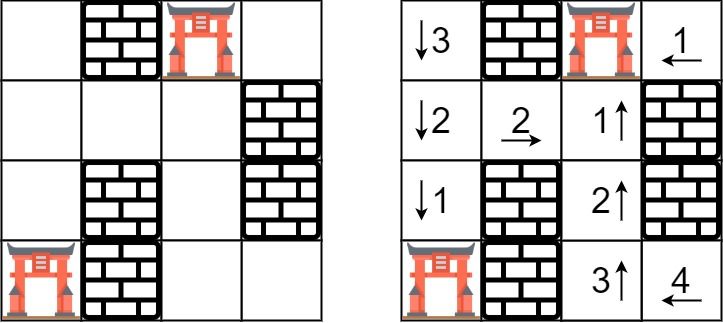
Input: rooms = [[2147483647,-1,0,2147483647],[2147483647,2147483647,2147483647,-1],[2147483647,-1,2147483647,-1],[0,-1,2147483647,2147483647]] Output: [[3,-1,0,1],[2,2,1,-1],[1,-1,2,-1],[0,-1,3,4]]
Example 2:
Input: rooms = [[-1]] Output: [[-1]]
Constraints:
m == rooms.lengthn == rooms[i].length1 <= m, n <= 250rooms[i][j]is-1,0, or231 - 1.
Solutions
This solution code is a solution for the problem where you are given a 2D grid rooms initialized with three possible values:
-1: A wall or an obstacle.0: A gate.INF(represented by2**31 - 1): An empty room. The goal is to fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should remainINF.
Methodology:
- Initialization:
- The dimensions of the grid are stored in
mandn. - A very large value (
inf = 2**31 - 1) is used to representINF, the initial state for empty rooms. - A queue
qis initialized with the positions of all gates in the grid. This queue will be used for a Breadth-First Search (BFS).
- The dimensions of the grid are stored in
- Breadth-First Search (BFS):
- The BFS starts from all gates simultaneously. This parallel start is crucial because it ensures that the search radiates uniformly from all gates, efficiently calculating the minimum distance to each gate for all rooms.
- With each iteration (
d += 1), the distance from the gates increases by 1. This distancedis used to update the rooms that are reached in this iteration. - For each position
(i, j)dequeued fromq, the algorithm checks its four adjacent positions. If an adjacent position(x, y)is within bounds and its value isinf(indicating an unvisited empty room), the room’s value is updated tod(the current distance from a gate), and(x, y)is added to the queue for further exploration in the next iteration.
- Updating Rooms:
- The grid
roomsis updated in-place, with each empty room getting the distance to its nearest gate. This is achieved by setting the value ofrooms[x][y]todwhen it is first reached in the BFS. Since the BFS ensures that the shortest path is found first (due to the queue processing elements in order of their insertion and distances increasing uniformly), each room is guaranteed to be assigned the shortest distance to a gate.
- The grid
- Termination:
- The BFS terminates when there are no more rooms to process (i.e., the queue
qbecomes empty). At this point, all reachable rooms have been assigned the shortest distance to a nearest gate.
- The BFS terminates when there are no more rooms to process (i.e., the queue
Key Points:
- The use of BFS from gates (as opposed to starting the search from each empty room and looking for a gate) is efficient and ensures the shortest paths are found without redundant calculations.
- This solution modifies the
roomsgrid in-place, effectively turning it into the result without needing additional space (apart from the space for the queue, which is relatively small). - The choice of
infas2**31 - 1is arbitrary but effectively represents a very large distance, assuming the grid sizes are reasonable and won’t exceed this distance.
-
class Solution { public void wallsAndGates(int[][] rooms) { int m = rooms.length; int n = rooms[0].length; Deque<int[]> q = new LinkedList<>(); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (rooms[i][j] == 0) { q.offer(new int[] {i, j}); } } } int d = 0; int[] dirs = {-1, 0, 1, 0, -1}; while (!q.isEmpty()) { ++d; for (int i = q.size(); i > 0; --i) { int[] p = q.poll(); for (int j = 0; j < 4; ++j) { int x = p[0] + dirs[j]; int y = p[1] + dirs[j + 1]; if (x >= 0 && x < m && y >= 0 && y < n && rooms[x][y] == Integer.MAX_VALUE) { rooms[x][y] = d; q.offer(new int[] {x, y}); } } } } } } -
class Solution { public: void wallsAndGates(vector<vector<int>>& rooms) { int m = rooms.size(); int n = rooms[0].size(); queue<pair<int, int>> q; for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) if (rooms[i][j] == 0) q.emplace(i, j); int d = 0; vector<int> dirs = {-1, 0, 1, 0, -1}; while (!q.empty()) { ++d; for (int i = q.size(); i > 0; --i) { auto p = q.front(); q.pop(); for (int j = 0; j < 4; ++j) { int x = p.first + dirs[j]; int y = p.second + dirs[j + 1]; if (x >= 0 && x < m && y >= 0 && y < n && rooms[x][y] == INT_MAX) { rooms[x][y] = d; q.emplace(x, y); } } } } } }; -
class Solution: def wallsAndGates(self, rooms: List[List[int]]) -> None: """ Do not return anything, modify rooms in-place instead. """ m, n = len(rooms), len(rooms[0]) inf = 2**31 - 1 q = deque([(i, j) for i in range(m) for j in range(n) if rooms[i][j] == 0]) d = 0 while q: d += 1 for _ in range(len(q)): i, j = q.popleft() for a, b in [[0, 1], [0, -1], [1, 0], [-1, 0]]: x, y = i + a, j + b # bfs so first reaching inf is always the shortest # set its value from inf to d, same as marking as visited if 0 <= x < m and 0 <= y < n and rooms[x][y] == inf: rooms[x][y] = d q.append((x, y)) ############ class Solution: # dfs def wallsAndGates(self, rooms: List[List[int]]) -> None: if not rooms or not rooms[0]: return m, n = len(rooms), len(rooms[0]) isVisited = [[False] * n for _ in range(m)] # isVisited map shared among all gates def fill(i: int, j: int, distance: int) -> None: nonlocal m, n # rooms[i][j] <= 0 meaning == -1 or == 0, both stop if i < 0 or i >= m or j < 0 or j >= n or rooms[i][j] <= 0 or isVisited[i][j]: return rooms[i][j] = min(rooms[i][j], distance) isVisited[i][j] = True fill(i - 1, j, distance + 1) fill(i, j + 1, distance + 1) fill(i + 1, j, distance + 1) fill(i, j - 1, distance + 1) isVisited[i][j] = False for i in range(m): for j in range(n): if rooms[i][j] == 0: # start from every gate fill(i, j, 0) ############ from collections import deque INF = 2147483647 class Solution(object): def wallsAndGates(self, rooms): """ :type rooms: List[List[int]] :rtype: void Do not return anything, modify rooms in-place instead. """ queue = deque([]) directions = [(1, 0), (-1, 0), (0, 1), (0, -1)] for i in range(0, len(rooms)): for j in range(0, len(rooms[0])): if rooms[i][j] == 0: queue.append((i, j)) while queue: i, j = queue.popleft() for di, dj in directions: p, q = i + di, j + dj if 0 <= p < len(rooms) and 0 <= q < len(rooms[0]) and rooms[p][q] == INF: rooms[p][q] = rooms[i][j] + 1 queue.append((p, q)) -
func wallsAndGates(rooms [][]int) { m, n := len(rooms), len(rooms[0]) var q [][]int for i := 0; i < m; i++ { for j := 0; j < n; j++ { if rooms[i][j] == 0 { q = append(q, []int{i, j}) } } } d := 0 dirs := []int{-1, 0, 1, 0, -1} for len(q) > 0 { d++ for i := len(q); i > 0; i-- { p := q[0] q = q[1:] for j := 0; j < 4; j++ { x, y := p[0]+dirs[j], p[1]+dirs[j+1] if x >= 0 && x < m && y >= 0 && y < n && rooms[x][y] == math.MaxInt32 { rooms[x][y] = d q = append(q, []int{x, y}) } } } } }