Welcome to Subscribe On Youtube
250. Count Univalue Subtrees
Description
Given the root of a binary tree, return the number of uni-value subtrees.
A uni-value subtree means all nodes of the subtree have the same value.
Example 1:
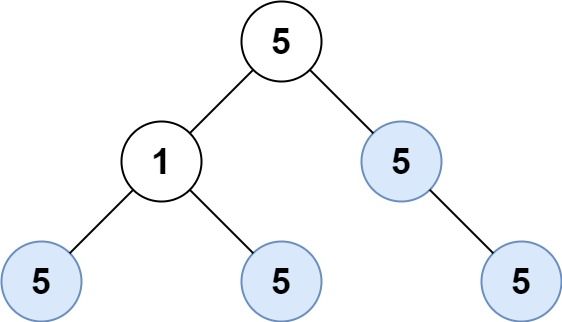
Input: root = [5,1,5,5,5,null,5] Output: 4
Example 2:
Input: root = [] Output: 0
Example 3:
Input: root = [5,5,5,5,5,null,5] Output: 6
Constraints:
- The number of the node in the tree will be in the range
[0, 1000]. -1000 <= Node.val <= 1000
Solutions
Check from bottom to top, using post-order traversal, left and right roots, we still call the function recursively.
For the currently traversed node, if the function is called recursively on the left and right child nodes, and the return is true.
Then it means that the value of the current node and the value of the left and right subtrees are the same, then there is another tree, so the result is incremented by 1.
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private int ans; public int countUnivalSubtrees(TreeNode root) { dfs(root); return ans; } private boolean dfs(TreeNode root) { if (root == null) { return true; } boolean l = dfs(root.left); boolean r = dfs(root.right); if (!l || !r) { return false; } int a = root.left == null ? root.val : root.left.val; int b = root.right == null ? root.val : root.right.val; if (a == b && b == root.val) { ++ans; return true; } return false; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int countUnivalSubtrees(TreeNode* root) { int ans = 0; function<bool(TreeNode*)> dfs = [&](TreeNode* root) -> bool { if (!root) { return true; } bool l = dfs(root->left); bool r = dfs(root->right); if (!l || !r) { return false; } int a = root->left ? root->left->val : root->val; int b = root->right ? root->right->val : root->val; if (a == b && b == root->val) { ++ans; return true; } return false; }; dfs(root); return ans; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def countUnivalSubtrees(self, root: TreeNode) -> int: count = 0 def is_unival(node): nonlocal count if not node: return True left_unival = is_unival(node.left) right_unival = is_unival(node.right) if left_unival and right_unival: if node.left and node.val != node.left.val: return False if node.right and node.val != node.right.val: return False count += 1 return True return False is_unival(root) return count class Solution: # return 2 values def countUnivalSubtrees(self, root: TreeNode) -> int: def is_unival(node): if not node: return True, 0 left_unival, left_count = is_unival(node.left) right_unival, right_count = is_unival(node.right) if left_unival and right_unival: if node.left and node.val != node.left.val: return False, 0 if node.right and node.val != node.right.val: return False, 0 return True, left_count + right_count + 1 return False, 0 _, count = is_unival(root) return count -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func countUnivalSubtrees(root *TreeNode) (ans int) { var dfs func(*TreeNode) bool dfs = func(root *TreeNode) bool { if root == nil { return true } l, r := dfs(root.Left), dfs(root.Right) if !l || !r { return false } if root.Left != nil && root.Left.Val != root.Val { return false } if root.Right != nil && root.Right.Val != root.Val { return false } ans++ return true } dfs(root) return } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function countUnivalSubtrees(root: TreeNode | null): number { let ans: number = 0; const dfs = (root: TreeNode | null): boolean => { if (root == null) { return true; } const l: boolean = dfs(root.left); const r: boolean = dfs(root.right); if (!l || !r) { return false; } if (root.left != null && root.left.val != root.val) { return false; } if (root.right != null && root.right.val != root.val) { return false; } ++ans; return true; }; dfs(root); return ans; } -
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number} */ var countUnivalSubtrees = function (root) { let ans = 0; const dfs = root => { if (!root) { return true; } const l = dfs(root.left); const r = dfs(root.right); if (!l || !r) { return false; } if (root.left && root.left.val !== root.val) { return false; } if (root.right && root.right.val !== root.val) { return false; } ++ans; return true; }; dfs(root); return ans; };