Welcome to Subscribe On Youtube
Question
Formatted question description: https://leetcode.ca/all/240.html
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:
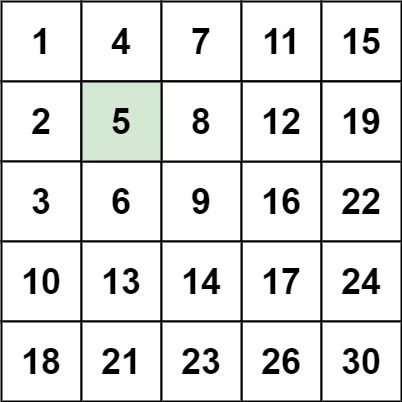
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 Output: true
Example 2:
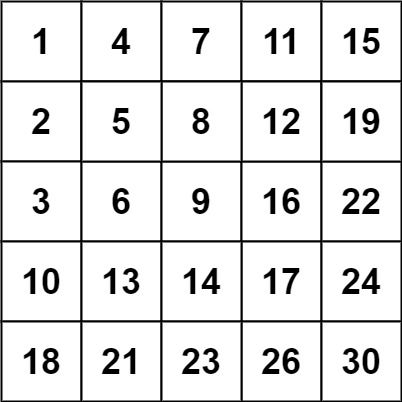
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
-109 <= target <= 109
Algorithm
It is an extension of the previous 74. Search a 2D Matrix.
74. Search a 2D Matrix is that the first number of each line is greater than the last number of the previous line. So for that question, you can expand the two-dimensional array into a one-bit array with a two-check search.
And this question has two unique numbers, the lower left corner and the upper right corner. The 18 in the lower left corner of above example, all the numbers going up become smaller, and all the numbers going to the right increase, then we can compare with the target number,
- If the number of targets is large, search to the right,
- If the target number is small, search upwards.
In this way, it can be judged whether the target number exists. Of course, we can also put the starting number in the upper right corner, search left and down, and set the stop condition correctly.
valid in Search_a_2D_Matrix, but not in II
{1, 4, 7, 11, 15},
{2, 5, 8, 12, 19},
Please refer to this comment, which is awesome https://leetcode.com/problems/search-a-2d-matrix-ii/discuss/66140/My-concise-O(m+n)-Java-solution/68155 .
Binary Search Variant
Performing a binary search in each row (or each column) for the target value. This approach takes advantage of the fact that elements in each row (and column) are sorted. Here’s how you can implement it in Python, performing a binary search across each row:
Time Complexity Analysis
- The binary search within a row takes
O(log n)time, wherenis the number of columns. - Performing this binary search for each of the m rows results in a total time complexity of
O(m log n).
This method can be particularly advantageous when the matrix is more row-heavy (i.e., many more rows than columns) or when you expect early termination due to finding the target in an early row. However, this approach does not fundamentally beat the O(m + n) complexity in the general case but offers an alternative strategy that might be situationally preferable.
Code
-
public class Search_a_2D_Matrix_II { public static void main(String[] args) { Search_a_2D_Matrix_II out = new Search_a_2D_Matrix_II(); Solution s = out.new Solution(); System.out.println(s.searchMatrix( new int[][]{ {1, 4, 7, 11, 15}, {2, 5, 8, 12, 19}, {3, 6, 9, 16, 22}, {10, 13, 14, 17, 24}, {18, 21, 23, 26, 30} }, 5 )); } /* valid in Search_a_2D_Matrix, but not in II {1, 4, 7, 11, 15}, {2, 5, 8, 12, 19}, */ class Solution { public boolean searchMatrix(int[][] matrix, int target) { if (matrix == null || matrix.length == 0 || matrix[0].length == 0) { return false; } int row = matrix.length; int col = matrix[0].length; int i = 0; int j = col - 1; while (i < row && j >= 0) { int val = matrix[i][j]; if (val == target) { return true; } else if (target < val) { j--; // all numbers in that column are even larger } else { i++; // all numbers in that row are even smaller } } return false; } } } ############ class Solution { public boolean searchMatrix(int[][] matrix, int target) { int m = matrix.length, n = matrix[0].length; int i = m - 1, j = 0; while (i >= 0 && j < n) { if (matrix[i][j] == target) { return true; } if (matrix[i][j] > target) { --i; } else { ++j; } } return false; } } -
// OJ: https://leetcode.com/problems/search-a-2d-matrix-ii/ // Time: O(M + N) // Space: O(1) class Solution { public: bool searchMatrix(vector<vector<int>>& A, int target) { int M = A.size(), N = A[0].size(), i = 0, j = N - 1; while (i < M && j >= 0) { if (A[i][j] == target) return true; if (A[i][j] < target) ++i; else --j; } return false; } }; -
# Binary Search Variant def binarySearch(row: List[int], target: int) -> bool: left, right = 0, len(row) - 1 while left <= right: mid = (left + right) // 2 if row[mid] == target: return True elif row[mid] < target: left = mid + 1 else: right = mid - 1 return False def searchMatrix(matrix: List[List[int]], target: int) -> bool: for row in matrix: if binarySearch(row, target): return True return False ############## # start from top-right corner class Solution: def searchMatrix(self, matrix: List[List[int]], target: int) -> bool: if not matrix or not matrix[0]: return False row, col = len(matrix), len(matrix[0]) i, j = 0, col - 1 while i < row and j >= 0: val = matrix[i][j] if val == target: return True elif target < val: j -= 1 # all numbers in that column are even larger else: i += 1 # all numbers in that row are even smaller return False # start from bottom-left corner class Solution: def searchMatrix(self, matrix: List[List[int]], target: int) -> bool: m, n = len(matrix), len(matrix[0]) i, j = m - 1, 0 while i >= 0 and j < n: if matrix[i][j] == target: return True if matrix[i][j] > target: i -= 1 else: j += 1 return False ############ class Solution(object): def searchMatrix(self, matrix, target): """ :type matrix: List[List[int]] :type target: int :rtype: bool """ def binarySearch(nums, target): start, end = 0, len(nums) - 1 while start + 1 < end: mid = start + (end - start) / 2 if nums[mid] > target: end = mid elif nums[mid] < target: start = mid else: return True if nums[start] == target: return True if nums[end] == target: return True return False for nums in matrix: if binarySearch(nums, target): return True return False -
func searchMatrix(matrix [][]int, target int) bool { m, n := len(matrix), len(matrix[0]) i, j := m-1, 0 for i >= 0 && j < n { if matrix[i][j] == target { return true } if matrix[i][j] > target { i-- } else { j++ } } return false } -
function searchMatrix(matrix: number[][], target: number): boolean { let m = matrix.length, n = matrix[0].length; let i = m - 1, j = 0; while (i >= 0 && j < n) { let cur = matrix[i][j]; if (cur == target) return true; if (cur > target) { --i; } else { ++j; } } return false; } -
/** * @param {number[][]} matrix * @param {number} target * @return {boolean} */ var searchMatrix = function (matrix, target) { const n = matrix[0].length; for (const row of matrix) { let left = 0, right = n; while (left < right) { const mid = (left + right) >> 1; if (row[mid] >= target) { right = mid; } else { left = mid + 1; } } if (left != n && row[left] == target) { return true; } } return false; }; -
public class Solution { public bool SearchMatrix(int[][] matrix, int target) { int m = matrix.Length, n = matrix[0].Length; int i = m - 1, j = 0; while (i >= 0 && j < n) { if (matrix[i][j] == target) { return true; } if (matrix[i][j] > target) { --i; } else { ++j; } } return false; } } -
use std::cmp::Ordering; impl Solution { pub fn search_matrix(matrix: Vec<Vec<i32>>, target: i32) -> bool { let m = matrix.len(); let n = matrix[0].len(); let mut i = 0; let mut j = n; while i < m && j > 0 { match target.cmp(&matrix[i][j - 1]) { Ordering::Less => j -= 1, Ordering::Greater => i += 1, Ordering::Equal => return true, } } false } }