Welcome to Subscribe On Youtube

119. Pascal’s Triangle II

Description

Given an integer rowIndex, return the rowIndexth (0-indexed) row of the Pascal's triangle.

In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:

 

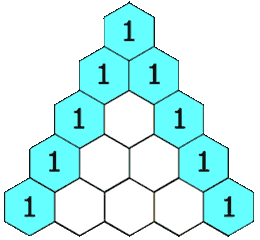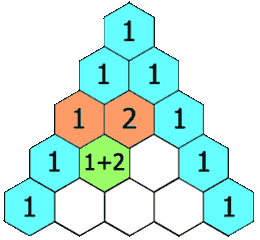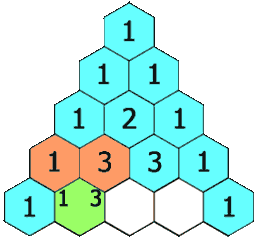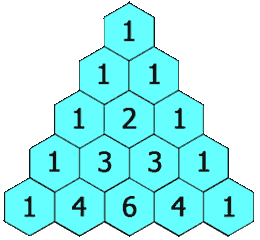
Example 1:

Input: rowIndex = 3
Output: [1,3,3,1]

Example 2:

Input: rowIndex = 0
Output: [1]

Example 3:

Input: rowIndex = 1
Output: [1,1]

 

Constraints:

• 0 <= rowIndex <= 33

 

Follow up: Could you optimize your algorithm to use only O(rowIndex) extra space?

Solutions

Solution 1: Recursion

We create an array $f$ of length $rowIndex + 1$, initially all elements are $1$.

Next, starting from the second row, we calculate the value of the $j$th element in the current row from back to front, $f[j] = f[j] + f[j - 1]$, where $j \in [1, i - 1]$.

Finally, return $f$.

The time complexity is $O(n^2)$, and the space complexity is $O(n)$. Here, $n$ is the given number of rows.

• Java
• C++
• Python
• Go
• TypeScript
• RenderScript

• class Solution {
      public List<Integer> getRow(int rowIndex) {
          List<Integer> f = new ArrayList<>();
          for (int i = 0; i < rowIndex + 1; ++i) {
              f.add(1);
          }
          for (int i = 2; i < rowIndex + 1; ++i) {
              for (int j = i - 1; j > 0; --j) {
                  f.set(j, f.get(j) + f.get(j - 1));
              }
          }
          return f;
      }
  }
  

• class Solution {
  public:
      vector<int> getRow(int rowIndex) {
          vector<int> f(rowIndex + 1, 1);
          for (int i = 2; i < rowIndex + 1; ++i) {
              for (int j = i - 1; j; --j) {
                  f[j] += f[j - 1];
              }
          }
          return f;
      }
  };
  

• class Solution:
      def getRow(self, rowIndex: int) -> List[int]:
          f = [1] * (rowIndex + 1)
          for i in range(2, rowIndex + 1):
              for j in range(i - 1, 0, -1):
                  f[j] += f[j - 1]
          return f
  
  

• func getRow(rowIndex int) []int {
  	f := make([]int, rowIndex+1)
  	for i := range f {
  		f[i] = 1
  	}
  	for i := 2; i < rowIndex+1; i++ {
  		for j := i - 1; j > 0; j-- {
  			f[j] += f[j-1]
  		}
  	}
  	return f
  }
  

• function getRow(rowIndex: number): number[] {
      const f: number[] = Array(rowIndex + 1).fill(1);
      for (let i = 2; i < rowIndex + 1; ++i) {
          for (let j = i - 1; j; --j) {
              f[j] += f[j - 1];
          }
      }
      return f;
  }
  
  

• impl Solution {
      pub fn get_row(row_index: i32) -> Vec<i32> {
          let n = (row_index + 1) as usize;
          let mut f = vec![1; n];
          for i in 2..n {
              for j in (1..i).rev() {
                  f[j] += f[j - 1];
              }
          }
          f
      }
  }
  
  

All Problems

All Solutions