97. Interleaving String

Description

Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.

An interleaving of two strings s and t is a configuration where s and t are divided into n and m substrings respectively, such that:

s = s₁ + s₂ + ... + s_n
t = t₁ + t₂ + ... + t_m
|n - m| <= 1
The interleaving is s₁ + t₁ + s₂ + t₂ + s₃ + t₃ + ... or t₁ + s₁ + t₂ + s₂ + t₃ + s₃ + ...

Note: a + b is the concatenation of strings a and b.

Example 1:

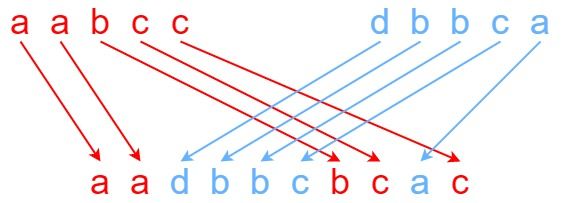
Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
Output: true
Explanation: One way to obtain s3 is:
Split s1 into s1 = "aa" + "bc" + "c", and s2 into s2 = "dbbc" + "a".
Interleaving the two splits, we get "aa" + "dbbc" + "bc" + "a" + "c" = "aadbbcbcac".
Since s3 can be obtained by interleaving s1 and s2, we return true.

Example 2:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
Output: false
Explanation: Notice how it is impossible to interleave s2 with any other string to obtain s3.

Example 3:

Input: s1 = "", s2 = "", s3 = ""
Output: true

Constraints:

0 <= s1.length, s2.length <= 100
0 <= s3.length <= 200
s1, s2, and s3 consist of lowercase English letters.

Follow up: Could you solve it using only O(s2.length) additional memory space?

Solutions

Solution 1: Memoization Search

Let’s denote the length of string $s_1$ as $m$ and the length of string $s_2$ as $n$. If $m + n \neq |s_3|$, then $s_3$ is definitely not an interleaving string of $s_1$ and $s_2$, so we return false.

Next, we design a function $dfs(i, j)$, which represents whether the remaining part of $s_3$ can be interleaved from the $i$th character of $s_1$ and the $j$th character of $s_2$. The answer is $dfs(0, 0)$.

The calculation process of function $dfs(i, j)$ is as follows:

If $i \geq m$ and $j \geq n$, it means that both $s_1$ and $s_2$ have been traversed, so we return true.

If $i < m$ and $s_1[i] = s_3[i + j]$, it means that the character $s_1[i]$ is part of $s_3[i + j]$. Therefore, we recursively call $dfs(i + 1, j)$ to check whether the next character of $s_1$ can match the current character of $s_2$. If it can match, we return true.

Similarly, if $j < n$ and $s_2[j] = s_3[i + j]$, it means that the character $s_2[j]$ is part of $s_3[i + j]$. Therefore, we recursively call $dfs(i, j + 1)$ to check whether the next character of $s_2$ can match the current character of $s_1$. If it can match, we return true.

Otherwise, we return false.

To avoid repeated calculations, we can use memoization search.

The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the lengths of strings $s_1$ and $s_2$ respectively.

Solution 2: Dynamic Programming

We can convert the memoization search in Solution 1 into dynamic programming.

We define $f[i][j]$ to represent whether the first $i$ characters of string $s_1$ and the first $j$ characters of string $s_2$ can interleave to form the first $i + j$ characters of string $s_3$. When transitioning states, we can consider whether the current character is obtained from the last character of $s_1$ or the last character of $s_2$. Therefore, we have the state transition equation:

\[f[i][j] = \begin{cases} f[i - 1][j] & \text{if } s_1[i - 1] = s_3[i + j - 1] \\ \text{or } f[i][j - 1] & \text{if } s_2[j - 1] = s_3[i + j - 1] \\ \text{false} & \text{otherwise} \end{cases}\]

where $f[0][0] = \text{true}$ indicates that an empty string is an interleaving string of two empty strings.

The answer is $f[m][n]$.

The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the lengths of strings $s_1$ and $s_2$ respectively.

We notice that the state $f[i][j]$ is only related to the states $f[i - 1][j]$, $f[i][j - 1]$, and $f[i - 1][j - 1]$. Therefore, we can use a rolling array to optimize the space complexity, reducing the original space complexity from $O(m \times n)$ to $O(n)$.

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        int m = s1.length(), n = s2.length();
        if (m + n != s3.length()) {
            return false;
        }
        boolean[] f = new boolean[n + 1];
        f[0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 0; j <= n; ++j) {
                int k = i + j - 1;
                if (i > 0) {
                    f[j] &= s1.charAt(i - 1) == s3.charAt(k);
                }
                if (j > 0) {
                    f[j] |= (f[j - 1] & s2.charAt(j - 1) == s3.charAt(k));
                }
            }
        }
        return f[n];
    }
}

//////

public class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        if (s1.length() == 0 || s1 == null) {
            return s2.equals(s3);
        }

        if (s2.length() == 0 || s2 == null) {
            return s1.equals(s3);
        }

        // @note: missed this simple check
        if (s1.length() + s2.length() != s3.length()) {
            return false;
        }

        // 1-to-i of s1, and 1-to-j of s2, can for 1-to-(i+j) of s3
        boolean[][] dp = new boolean[s1.length() + 1][s2.length() + 1]; // +1 for empty string

        dp[0][0] = true;

        // pre-process for empty string case
        for (int i = 1; i < s1.length() + 1; i++) {
            dp[i][0] = (s1.charAt(i - 1) == s3.charAt(i - 1))
                && dp[i - 1][0];
        }
        for (int i = 1; i < s2.length() + 1; i++) {
            dp[0][i] = (s2.charAt(i - 1) == s3.charAt(i - 1))
                && dp[0][i - 1];
        }

        for (int i = 1; i < s1.length() + 1; i++) {
            for (int j = 1; j < s2.length() + 1; j++) {

                boolean withS1 = s1.charAt(i - 1) == s3.charAt(i - 1 + j) && dp[i - 1][j];
                boolean withS2 = s2.charAt(j - 1) == s3.charAt(i - 1 + j) && dp[i][j - 1];

                dp[i][j] = withS1 || withS2;
            }
        }

        return dp[s1.length()][s2.length()];
    }
}

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m = s1.size(), n = s2.size();
        if (m + n != s3.size()) {
            return false;
        }
        bool f[n + 1];
        memset(f, false, sizeof(f));
        f[0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 0; j <= n; ++j) {
                int k = i + j - 1;
                if (i) {
                    f[j] &= s1[i - 1] == s3[k];
                }
                if (j) {
                    f[j] |= (s2[j - 1] == s3[k] && f[j - 1]);
                }
            }
        }
        return f[n];
    }
};

# 2-d
class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        if len(s1) + len(s2) != len(s3):
            return False

        dp = [[False] * (len(s2) + 1) for _ in range(len(s1) + 1)]
        dp[0][0] = True

        for i in range(1, len(s1) + 1):
            dp[i][0] = s1[i - 1] == s3[i - 1] and dp[i - 1][0]
        for i in range(1, len(s2) + 1):
            dp[0][i] = s2[i - 1] == s3[i - 1] and dp[0][i - 1]

        # fill in dp array
        for i in range(1, len(s1) + 1):
            for j in range(1, len(s2) + 1):
                with_s1 = s1[i - 1] == s3[i + j - 1] and dp[i - 1][j]
                with_s2 = s2[j - 1] == s3[i + j - 1] and dp[i][j - 1]
                dp[i][j] = with_s1 or with_s2

        return dp[-1][-1]

############

# 1-d
class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        m, n = len(s1), len(s2)
        if m + n != len(s3):
            return False
        f = [True] + [False] * n
        for i in range(m + 1):
            for j in range(n + 1):
                k = i + j - 1
                if i:
                    f[j] &= s1[i - 1] == s3[k]
                if j:
                    f[j] |= f[j - 1] and s2[j - 1] == s3[k]
        return f[n]

###########

class Solution: # dfs
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        m, n = len(s1), len(s2)
        if m + n != len(s3):
            return False

        @cache
        def dfs(i, j):
            if i == m and j == n:
                return True

            return (
                ( i < m and s1[i] == s3[i + j] and dfs(i + 1, j) )
                or
                ( j < n and s2[j] == s3[i + j] and dfs(i, j + 1) )
            )

        return dfs(0, 0)

func isInterleave(s1 string, s2 string, s3 string) bool {
	m, n := len(s1), len(s2)
	if m+n != len(s3) {
		return false
	}
	f := make([]bool, n+1)
	f[0] = true
	for i := 0; i <= m; i++ {
		for j := 0; j <= n; j++ {
			k := i + j - 1
			if i > 0 {
				f[j] = (f[j] && s1[i-1] == s3[k])
			}
			if j > 0 {
				f[j] = (f[j] || (s2[j-1] == s3[k] && f[j-1]))
			}
		}
	}
	return f[n]
}

function isInterleave(s1: string, s2: string, s3: string): boolean {
    const m = s1.length;
    const n = s2.length;
    if (m + n !== s3.length) {
        return false;
    }
    const f: boolean[] = new Array(n + 1).fill(false);
    f[0] = true;
    for (let i = 0; i <= m; ++i) {
        for (let j = 0; j <= n; ++j) {
            const k = i + j - 1;
            if (i) {
                f[j] = f[j] && s1[i - 1] === s3[k];
            }
            if (j) {
                f[j] = f[j] || (f[j - 1] && s2[j - 1] === s3[k]);
            }
        }
    }
    return f[n];
}

public class Solution {
    public bool IsInterleave(string s1, string s2, string s3) {
        int m = s1.Length, n = s2.Length;
        if (m + n != s3.Length) {
            return false;
        }
        bool[] f = new bool[n + 1];
        f[0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 0; j <= n; ++j) {
                int k = i + j - 1;
                if (i > 0) {
                    f[j] &= s1[i - 1] == s3[k];
                }
                if (j > 0) {
                    f[j] |= (f[j - 1] & s2[j - 1] == s3[k]);
                }
            }
        }
        return f[n];
    }
}

impl Solution {
    #[allow(dead_code)]
    pub fn is_interleave(s1: String, s2: String, s3: String) -> bool {
        let n = s1.len();
        let m = s2.len();

        if s1.len() + s2.len() != s3.len() {
            return false;
        }

        let mut record = vec![vec![-1; m + 1]; n + 1];

        Self::dfs(
            &mut record,
            n,
            m,
            0,
            0,
            &s1.chars().collect(),
            &s2.chars().collect(),
            &s3.chars().collect()
        )
    }

    #[allow(dead_code)]
    fn dfs(
        record: &mut Vec<Vec<i32>>,
        n: usize,
        m: usize,
        i: usize,
        j: usize,
        s1: &Vec<char>,
        s2: &Vec<char>,
        s3: &Vec<char>
    ) -> bool {
        if i >= n && j >= m {
            return true;
        }

        if record[i][j] != -1 {
            return record[i][j] == 1;
        }

        // Set the initial value
        record[i][j] = 0;
        let k = i + j;

        // Let's try `s1` first
        if i < n && s1[i] == s3[k] && Self::dfs(record, n, m, i + 1, j, s1, s2, s3) {
            record[i][j] = 1;
        }

        // If the first approach does not succeed, let's then try `s2`
        if
            record[i][j] == 0 &&
            j < m &&
            s2[j] == s3[k] &&
            Self::dfs(record, n, m, i, j + 1, s1, s2, s3)
        {
            record[i][j] = 1;
        }

        record[i][j] == 1
    }
}

97 - Interleaving String

97. Interleaving String

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

97. Interleaving String

Description

Solutions

All Problems

All Solutions