74. Search a 2D Matrix

Description

You are given an m x n integer matrix matrix with the following two properties:

Each row is sorted in non-decreasing order.
The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Example 1:

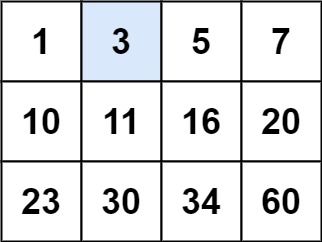
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

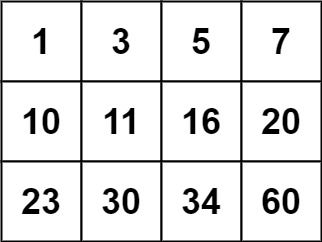
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-10⁴ <= matrix[i][j], target <= 10⁴

Solutions

Solution 1: Binary Search

We can logically unfold the two-dimensional matrix and then perform binary search.

The time complexity is $O(\log(m \times n))$, where $m$ and $n$ are the number of rows and columns of the matrix, respectively. The space complexity is $O(1)$.

Solution 2: Search from the Bottom Left or Top Right

Here, we start searching from the bottom left corner and move towards the top right direction. We compare the current element $matrix[i][j]$ with $target$:

If $matrix[i][j] = target$, we have found the target value and return true.
If $matrix[i][j] > target$, all elements to the right of the current position in this row are greater than target, so we should move the pointer $i$ upwards, i.e., $i = i - 1$.
If $matrix[i][j] < target$, all elements above the current position in this column are less than target, so we should move the pointer $j$ to the right, i.e., $j = j + 1$.

If we still can’t find $target$ after the search, return false.

The time complexity is $O(m + n)$, where $m$ and $n$ are the number of rows and columns of the matrix, respectively. The space complexity is $O(1)$.

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int left = 0, right = m * n - 1;
        while (left < right) {
            int mid = (left + right) >> 1;
            int x = mid / n, y = mid % n;
            if (matrix[x][y] >= target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return matrix[left / n][left % n] == target;
    }
}

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int left = 0, right = m * n - 1;
        while (left < right) {
            int mid = left + right >> 1;
            int x = mid / n, y = mid % n;
            if (matrix[x][y] >= target) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return matrix[left / n][left % n] == target;
    }
};

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
        left, right = 0, m * n - 1
        while left <= right: # must be <=, not <, for matrax=[[1]],target=1
            mid = (left + right) >> 1
            x, y = divmod(mid, n) # note: divide column count
            if matrix[x][y] == target:
                return True
            elif matrix[x][y] > target:
                right = mid - 1
            else:
                left = mid + 1
        return False

###########

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
        left, right = 0, m * n - 1
        while left < right:
            mid = (left + right) >> 1
            x, y = divmod(mid, n)
            if matrix[x][y] >= target:
                right = mid
            else:
                left = mid + 1
        return matrix[left // n][left % n] == target

func searchMatrix(matrix [][]int, target int) bool {
	m, n := len(matrix), len(matrix[0])
	left, right := 0, m*n-1
	for left < right {
		mid := (left + right) >> 1
		x, y := mid/n, mid%n
		if matrix[x][y] >= target {
			right = mid
		} else {
			left = mid + 1
		}
	}
	return matrix[left/n][left%n] == target
}

function searchMatrix(matrix: number[][], target: number): boolean {
    const m = matrix.length;
    const n = matrix[0].length;
    let left = 0;
    let right = m * n;
    while (left < right) {
        const mid = (left + right) >>> 1;
        const i = Math.floor(mid / n);
        const j = mid % n;
        if (matrix[i][j] === target) {
            return true;
        }

        if (matrix[i][j] < target) {
            left = mid + 1;
        } else {
            right = mid;
        }
    }
    return false;
}

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
    const m = matrix.length,
        n = matrix[0].length;
    let left = 0,
        right = m * n - 1;
    while (left < right) {
        const mid = (left + right + 1) >> 1;
        const x = Math.floor(mid / n);
        const y = mid % n;
        if (matrix[x][y] <= target) {
            left = mid;
        } else {
            right = mid - 1;
        }
    }
    return matrix[Math.floor(left / n)][left % n] == target;
};

use std::cmp::Ordering;
impl Solution {
    pub fn search_matrix(matrix: Vec<Vec<i32>>, target: i32) -> bool {
        let m = matrix.len();
        let n = matrix[0].len();
        let mut i = 0;
        let mut j = n;
        while i < m && j > 0 {
            match matrix[i][j - 1].cmp(&target) {
                Ordering::Equal => {
                    return true;
                }
                Ordering::Less => {
                    i += 1;
                }
                Ordering::Greater => {
                    j -= 1;
                }
            }
        }
        false
    }
}

74 - Search a 2D Matrix

74. Search a 2D Matrix

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

74. Search a 2D Matrix

Description

Solutions

All Problems

All Solutions