Welcome to Subscribe On Youtube
64. Minimum Path Sum
Description
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
Example 1:
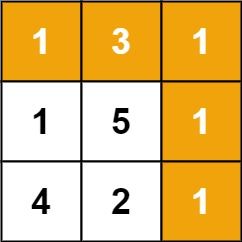
Input: grid = [[1,3,1],[1,5,1],[4,2,1]] Output: 7 Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.
Example 2:
Input: grid = [[1,2,3],[4,5,6]] Output: 12
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 200
Solutions
Solution 1: Dynamic Programming
We define $f[i][j]$ to represent the minimum path sum from the top left corner to $(i, j)$. Initially, $f[0][0] = grid[0][0]$, and the answer is $f[m - 1][n - 1]$.
Consider $f[i][j]$:
- If $j = 0$, then $f[i][j] = f[i - 1][j] + grid[i][j]$;
- If $i = 0$, then $f[i][j] = f[i][j - 1] + grid[i][j]$;
- If $i > 0$ and $j > 0$, then $f[i][j] = \min(f[i - 1][j], f[i][j - 1]) + grid[i][j]$.
Finally, return $f[m - 1][n - 1]$.
The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the number of rows and columns of the grid, respectively.
-
class Solution { public int minPathSum(int[][] grid) { int m = grid.length, n = grid[0].length; int[][] f = new int[m][n]; f[0][0] = grid[0][0]; for (int i = 1; i < m; ++i) { f[i][0] = f[i - 1][0] + grid[i][0]; } for (int j = 1; j < n; ++j) { f[0][j] = f[0][j - 1] + grid[0][j]; } for (int i = 1; i < m; ++i) { for (int j = 1; j < n; ++j) { f[i][j] = Math.min(f[i - 1][j], f[i][j - 1]) + grid[i][j]; } } return f[m - 1][n - 1]; } } -
class Solution { public: int minPathSum(vector<vector<int>>& grid) { int m = grid.size(), n = grid[0].size(); int f[m][n]; f[0][0] = grid[0][0]; for (int i = 1; i < m; ++i) { f[i][0] = f[i - 1][0] + grid[i][0]; } for (int j = 1; j < n; ++j) { f[0][j] = f[0][j - 1] + grid[0][j]; } for (int i = 1; i < m; ++i) { for (int j = 1; j < n; ++j) { f[i][j] = min(f[i - 1][j], f[i][j - 1]) + grid[i][j]; } } return f[m - 1][n - 1]; } }; -
class Solution: def minPathSum(self, grid: List[List[int]]) -> int: m, n = len(grid), len(grid[0]) f = [[0] * n for _ in range(m)] f[0][0] = grid[0][0] for i in range(1, m): f[i][0] = f[i - 1][0] + grid[i][0] for j in range(1, n): f[0][j] = f[0][j - 1] + grid[0][j] for i in range(1, m): for j in range(1, n): f[i][j] = min(f[i - 1][j], f[i][j - 1]) + grid[i][j] return f[-1][-1] -
func minPathSum(grid [][]int) int { m, n := len(grid), len(grid[0]) f := make([][]int, m) for i := range f { f[i] = make([]int, n) } f[0][0] = grid[0][0] for i := 1; i < m; i++ { f[i][0] = f[i-1][0] + grid[i][0] } for j := 1; j < n; j++ { f[0][j] = f[0][j-1] + grid[0][j] } for i := 1; i < m; i++ { for j := 1; j < n; j++ { f[i][j] = min(f[i-1][j], f[i][j-1]) + grid[i][j] } } return f[m-1][n-1] } -
function minPathSum(grid: number[][]): number { const m = grid.length; const n = grid[0].length; const f: number[][] = Array(m) .fill(0) .map(() => Array(n).fill(0)); f[0][0] = grid[0][0]; for (let i = 1; i < m; ++i) { f[i][0] = f[i - 1][0] + grid[i][0]; } for (let j = 1; j < n; ++j) { f[0][j] = f[0][j - 1] + grid[0][j]; } for (let i = 1; i < m; ++i) { for (let j = 1; j < n; ++j) { f[i][j] = Math.min(f[i - 1][j], f[i][j - 1]) + grid[i][j]; } } return f[m - 1][n - 1]; } -
/** * @param {number[][]} grid * @return {number} */ var minPathSum = function (grid) { const m = grid.length; const n = grid[0].length; const f = Array(m) .fill(0) .map(() => Array(n).fill(0)); f[0][0] = grid[0][0]; for (let i = 1; i < m; ++i) { f[i][0] = f[i - 1][0] + grid[i][0]; } for (let j = 1; j < n; ++j) { f[0][j] = f[0][j - 1] + grid[0][j]; } for (let i = 1; i < m; ++i) { for (let j = 1; j < n; ++j) { f[i][j] = Math.min(f[i - 1][j], f[i][j - 1]) + grid[i][j]; } } return f[m - 1][n - 1]; }; -
public class Solution { public int MinPathSum(int[][] grid) { int m = grid.Length, n = grid[0].Length; int[,] f = new int[m, n]; f[0, 0] = grid[0][0]; for (int i = 1; i < m; ++i) { f[i, 0] = f[i - 1, 0] + grid[i][0]; } for (int j = 1; j < n; ++j) { f[0, j] = f[0, j - 1] + grid[0][j]; } for (int i = 1; i < m; ++i) { for (int j = 1; j < n; ++j) { f[i, j] = Math.Min(f[i - 1, j], f[i, j - 1]) + grid[i][j]; } } return f[m - 1, n - 1]; } } -
impl Solution { pub fn min_path_sum(mut grid: Vec<Vec<i32>>) -> i32 { let m = grid.len(); let n = grid[0].len(); for i in 1..m { grid[i][0] += grid[i - 1][0]; } for i in 1..n { grid[0][i] += grid[0][i - 1]; } for i in 1..m { for j in 1..n { grid[i][j] += grid[i][j - 1].min(grid[i - 1][j]); } } grid[m - 1][n - 1] } }