Welcome to Subscribe On Youtube
51. N-Queens
Description
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
Example 1:
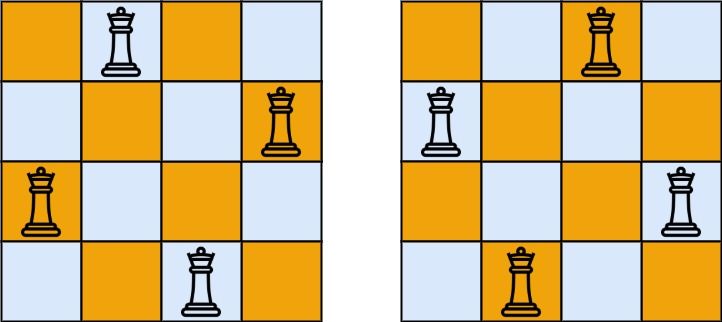
Input: n = 4 Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Example 2:
Input: n = 1 Output: [["Q"]]
Constraints:
1 <= n <= 9
Solutions
Solution 1: DFS (Backtracking)
We define three arrays $col$, $dg$, and $udg$ to represent whether there is a queen in the column, the main diagonal, and the anti-diagonal, respectively. If there is a queen at position $(i, j)$, then $col[j]$, $dg[i + j]$, and $udg[n - i + j]$ are all $1$. In addition, we use an array $g$ to record the current state of the chessboard, where all elements in $g$ are initially '.'.
Next, we define a function $dfs(i)$, which represents placing queens starting from the $i$th row.
In $dfs(i)$, if $i = n$, it means that we have completed the placement of all queens. We put the current $g$ into the answer array and end the recursion.
Otherwise, we enumerate each column $j$ of the current row. If there is no queen at position $(i, j)$, that is, $col[j]$, $dg[i + j]$, and $udg[n - i + j]$ are all $0$, then we can place a queen, that is, change $g[i][j]$ to 'Q', and set $col[j]$, $dg[i + j]$, and $udg[n - i + j]$ to $1$. Then we continue to search the next row, that is, call $dfs(i + 1)$. After the recursion ends, we need to change $g[i][j]$ back to '.' and set $col[j]$, $dg[i + j]$, and $udg[n - i + j]$ to $0$.
In the main function, we call $dfs(0)$ to start recursion, and finally return the answer array.
The time complexity is $O(n^2 \times n!)$, and the space complexity is $O(n)$. Here, $n$ is the integer given in the problem.
-
class Solution { private List<List<String>> ans = new ArrayList<>(); private int[] col; private int[] dg; private int[] udg; private String[][] g; private int n; public List<List<String>> solveNQueens(int n) { this.n = n; col = new int[n]; dg = new int[n << 1]; udg = new int[n << 1]; g = new String[n][n]; for (int i = 0; i < n; ++i) { Arrays.fill(g[i], "."); } dfs(0); return ans; } private void dfs(int i) { if (i == n) { List<String> t = new ArrayList<>(); for (int j = 0; j < n; ++j) { t.add(String.join("", g[j])); } ans.add(t); return; } for (int j = 0; j < n; ++j) { if (col[j] + dg[i + j] + udg[n - i + j] == 0) { g[i][j] = "Q"; col[j] = dg[i + j] = udg[n - i + j] = 1; dfs(i + 1); col[j] = dg[i + j] = udg[n - i + j] = 0; g[i][j] = "."; } } } } -
class Solution { public: vector<vector<string>> solveNQueens(int n) { vector<int> col(n); vector<int> dg(n << 1); vector<int> udg(n << 1); vector<vector<string>> ans; vector<string> t(n, string(n, '.')); function<void(int)> dfs = [&](int i) -> void { if (i == n) { ans.push_back(t); return; } for (int j = 0; j < n; ++j) { if (col[j] + dg[i + j] + udg[n - i + j] == 0) { t[i][j] = 'Q'; col[j] = dg[i + j] = udg[n - i + j] = 1; dfs(i + 1); col[j] = dg[i + j] = udg[n - i + j] = 0; t[i][j] = '.'; } } }; dfs(0); return ans; } }; -
class Solution: def solveNQueens(self, n: int) -> List[List[str]]: def dfs(i: int): if i == n: ans.append(["".join(row) for row in g]) return for j in range(n): if col[j] + dg[i + j] + udg[n - i + j] == 0: g[i][j] = "Q" col[j] = dg[i + j] = udg[n - i + j] = 1 dfs(i + 1) col[j] = dg[i + j] = udg[n - i + j] = 0 g[i][j] = "." ans = [] g = [["."] * n for _ in range(n)] col = [0] * n dg = [0] * (n << 1) udg = [0] * (n << 1) dfs(0) return ans -
func solveNQueens(n int) (ans [][]string) { col := make([]int, n) dg := make([]int, n<<1) udg := make([]int, n<<1) t := make([][]byte, n) for i := range t { t[i] = make([]byte, n) for j := range t[i] { t[i][j] = '.' } } var dfs func(int) dfs = func(i int) { if i == n { tmp := make([]string, n) for i := range tmp { tmp[i] = string(t[i]) } ans = append(ans, tmp) return } for j := 0; j < n; j++ { if col[j]+dg[i+j]+udg[n-i+j] == 0 { col[j], dg[i+j], udg[n-i+j] = 1, 1, 1 t[i][j] = 'Q' dfs(i + 1) t[i][j] = '.' col[j], dg[i+j], udg[n-i+j] = 0, 0, 0 } } } dfs(0) return } -
function solveNQueens(n: number): string[][] { const col: number[] = new Array(n).fill(0); const dg: number[] = new Array(n << 1).fill(0); const udg: number[] = new Array(n << 1).fill(0); const ans: string[][] = []; const t: string[][] = Array(n) .fill(0) .map(() => Array(n).fill('.')); const dfs = (i: number) => { if (i === n) { ans.push(t.map(x => x.join(''))); return; } for (let j = 0; j < n; ++j) { if (col[j] + dg[i + j] + udg[n - i + j] === 0) { t[i][j] = 'Q'; col[j] = dg[i + j] = udg[n - i + j] = 1; dfs(i + 1); col[j] = dg[i + j] = udg[n - i + j] = 0; t[i][j] = '.'; } } }; dfs(0); return ans; } -
public class Solution { private int n; private int[] col; private int[] dg; private int[] udg; private IList<IList<string>> ans = new List<IList<string>>(); private IList<string> t = new List<string>(); public IList<IList<string>> SolveNQueens(int n) { this.n = n; col = new int[n]; dg = new int[n << 1]; udg = new int[n << 1]; dfs(0); return ans; } private void dfs(int i) { if (i == n) { ans.Add(new List<string>(t)); return; } for (int j = 0; j < n; ++j) { if (col[j] + dg[i + j] + udg[n - i + j] == 0) { char[] row = new char[n]; Array.Fill(row, '.'); row[j] = 'Q'; t.Add(new string(row)); col[j] = dg[i + j] = udg[n - i + j] = 1; dfs(i + 1); col[j] = dg[i + j] = udg[n - i + j] = 0; t.RemoveAt(t.Count - 1); } } } }